Solving a Heptic Equation Without Using the Heptic Formula

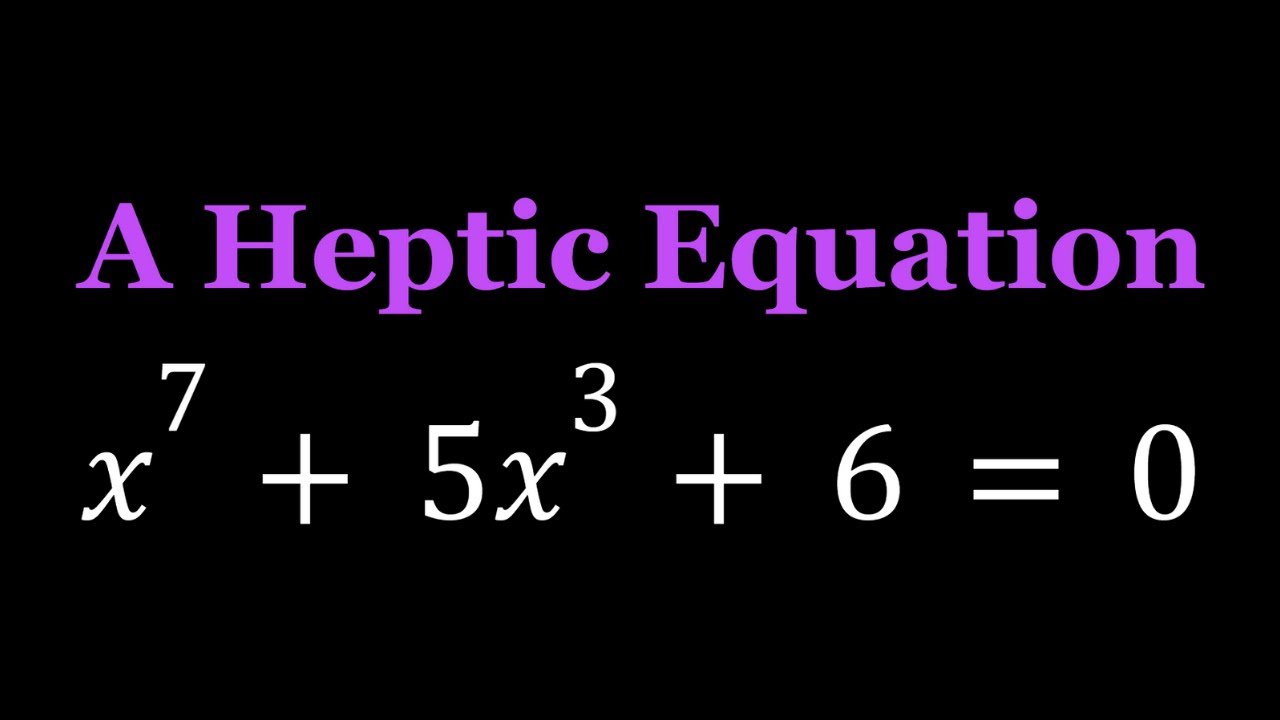
Показать описание

If you need to post a picture of your solution or idea:
#ChallengingMathProblems #PolynomialEquations
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva

PLAYLISTS 🎵 :

SyberMath

Рекомендации по теме

Комментарии

Another shorter solution:
1. It is obvious that -1 is a solutions since the sum of odd power coefficients equal the sum of even power coefficients.
2. We take the first derivative of f(x) and we find out that it is always positive, thus the function is increasing, thus it has only one solution in the real world.

georget

I want you to solve the equation over complex field

lroduzn

Given:
x⁷ + 5x³ + 6 = 0
To find:
x

By inspection, x = –1 is a solution (sum of odd powers = 1 + 0 + 5 + 0 = 0 + 0 + 0 + 6 = sum of even powers)

As the function only has odd powers of x, and as it only has positive coefficients, it is always increasing (f'(x) > 0)

Thus, x = – 1 is the only solution.

GirishManjunathMusic

Here is another way to solve it.

You can see that (for real solutions at least) the equation can only have negative solutions. Because x^7 + 5x^3 = -6, obviously no positive value of x will ever satisfy that.

Using the RRT you can find -1 as a solution.

Factor that out to get the long sixth-degree polynomial x^6 – x^5 + x^4 – x^3 + 6x^2 – 6x + 6 = 0

put the 6 on the other side and then factor it with (x - 1)

(x-1)x^5 + (x-1)x^3 + 6(x-1)x = -6

(x-1)(x^5 + x^3 + 6x) = -6

now factor an x out

x(x-1)(x^4 + x^2 + 6) = -6

so you have 3 parts to this equation now on the LHS:

x, x-1, and x^4 + x^2 + 6

their product must be negative 6. But their product can't be negative when x < 0 (which we already established must be true for all real solutions)

x will be negative

x - 1 will be negative

x^4 + x^2 + 6 of course will always be positive

negative * negative * positive = positive != -6

that contradiction shows there are no more real solutions

armacham

Here is another polynomial equation to solve (find all roots, real or complex):
x^6 + x^5 + x + 1 = 0
Hint: It is not necessary to directly solve a quartic equation if you figure out a trick

XJWill

It looks like x=-1 is a solution and we can use long division (so painful) to find the other factors not x+1
But....
about 10 and some minutes later
...
awesome!

SuperYoonHo

Videos like this never seem to utilize synthetic division, which, in this case, quickly yields the factorization of the polynomial over the reals. I, too, would very much like to see the complex solutions. I'm not even sure if the sextic is solvable by radicals.

wkbj

The equation can be expressed as x^3(x^4 + 5) = -6. The left hand side is a curve crossing x = 0 monotonically increasing, the right hand side is a horizontal line y = -6, they intersect at a unique point x = -1, the only real solution to the equation, the other 6 solutions are therefore three pairs of complex numbers.

seegeeaye

What was the point of the inflexion point and the second derivative? It’s completely irrelevant.

f(-1E6)<0, f(1E6)>0, so from Intermediate Value Theorem, there exists y where f(y) =0. Since f’(x)>=0 for all x, therefore only one real solution. x = -1 works, so therefore only real answer.

The same is true for any ax^m + bx^n = a + b where m and n are odd numbers, no matter how large.

MrLidless

Syber : Totally love your videos. This one was a time-waster though, because the title was so imprecise. Obviously, there's no Heptic formula, but the phrase "solving an equation" usually means finding ALL roots. Here you only wanted all REAL roots. Much easier. I quickly had (x+1) as a factor and divided it out by long division ( Not so hard. Took two minutes ); but then I tried to solve the hexic or factor further for another 45 minutes.

garyw.

Before watching the Vid.

=>Using the RRT(Rational Root Theorem) we can see the possible solutions in the given eqn are, ±1 ±2 ±3 and ±6
=>Input all of these Possible Solutions and we can see that -1 ONLY works, thus (x+1) is a factor leading to
(x+1)(x⁶+(....)+6)= x⁷ + 5x³ + 6
=>I'm gonna skip ahead of dividing x+1 from x⁷+5x³+6, and will gonna end up with x⁶-x⁵+x⁴-x³+6x²-6x+6
=>Looking at this Sixth-Degree Polynomial, we can see it DOESNT have Real roots at all, because using the RRT, we can see that 1, ±2, ±3, and ±6 (excluding -1, because we theorized it previously) arent compatible
=> Thus x= -1 is the only Integer Solution

threstytorres

Dear Sir
To find critical points of a function in single variable you equate the first derivative with zero not the 2nd derivative!!!

ahmadjaradat

The polynomial (x^7+5*x^3+6)/(x+1) is not solvable by radicals (using Pari-gp we take, its Galois groups is S_6, roots the most possible complicated)

elkincampos