filmov
tv
Solving 3^x+x^3=17, a Non-Standard Equation

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ExponentialEquations #NonStandard
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
#ChallengingMathProblems #ExponentialEquations #NonStandard
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
Solving 3^x+x^3=17, a Non-Standard Equation
Solving A Non-Standard Equation
A Non-Standard Equation with One Solution (k is positive)
Solving a Non-standard Exponential Equation
Solving a Non-Standard Radical Equation
Solving an equation with variables on both side and one solution
Solving (x-1)^2-x^3=17, a Polynomial Equation
Solving 2^x=x+(1/x), a Non-Standard Equation
J.E.D.I. Training MATH for DIGITAL SAT - Day 6 of 7 (37 Digital SAT Math Problems EXPLAINED)
Solving a quintic equation with a non-standard method. An algebraic challenge.
Solving an equation for y and x
Solving a Functional Equation in Non Standard Way
How to Solve One-Step Equations | One-Step Equation Steps | Math with Mr. J
How To Solve Absolute Value Equations, Basic Introduction, Algebra
Solving this equation a pretty non-standard way
Solving a radical equation. Algebra challenge.
Trigonometry: Solving a Trigonometric Equation, Quadratic in Form
Solving an equation for y and x using two steps
Solving an Exponential Equation
How to find the center and radius of a circle in standard form
Solving a Non-Standard Exponential Equation | x^x^2 + 6x + 8 = 1
Can You Solve this Rational Equation? | Quick & Easy Explanation
How to Solve and Equation for X: x(5x - 2) = 3 (a MATH 1010 Problem)
Solve the Quadratic Equation, 3x^2+3=-x, Using the Quadratic Formula (Two Complex Number Solutions)
Комментарии
 0:04:26
0:04:26
 0:09:05
0:09:05
 0:08:42
0:08:42
 0:07:28
0:07:28
 0:10:11
0:10:11
 0:02:36
0:02:36
 0:06:02
0:06:02
 0:10:18
0:10:18
 1:04:45
1:04:45
 0:09:49
0:09:49
 0:03:47
0:03:47
 0:08:08
0:08:08
 0:06:54
0:06:54
 0:04:21
0:04:21
 0:06:40
0:06:40
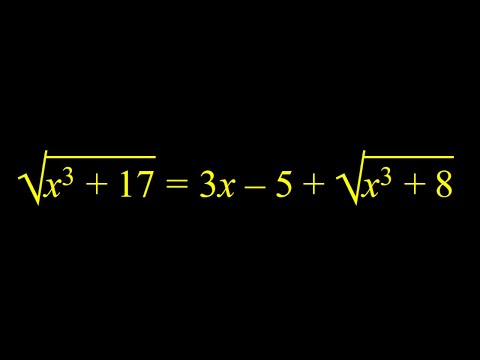 0:10:09
0:10:09
 0:06:36
0:06:36
 0:03:12
0:03:12
 0:00:56
0:00:56
 0:05:06
0:05:06
 0:08:18
0:08:18
 0:09:53
0:09:53
 0:05:17
0:05:17
 0:05:11
0:05:11