filmov
tv
Solving a Nice Polynomial System in Two Ways

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #PolynomialEquations #PolynomialSystems
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
#ChallengingMathProblems #PolynomialEquations #PolynomialSystems
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
Solving a Nice Polynomial System in Two Ways
Solving a Nice Polynomial System in Two Ways
Solving a Nice Polynomial System in Two Ways
Solving A Nice Polynomial System | Algebra
Solving A Nice Polynomial System | Two Ways
A Nice Polynomial System #algebra
Let's Solve A Nice Polynomial System
A Nice Polynomial System
Towards Deterministic Algorithms for Constant-Depth Factors of Constant-Depth Circuits
A Nice Polynomial System
I Solved A Nice Polynomial System
A Nice Polynomial System
Solving A Nice Polynomial System by Math26039335
Solving a Nice Polynomial Equation
A Nice Polynomial System by Stanley Rabinowitz
A Very Nice Polynomial System
A Nice Polynomial Equation | Algebra
Let's Solve A Nice Polynomial Equation | Math Olympiads
A Nice Polynomial System Solved in Three Ways
Solving A Polynomial System
Solving A Real Polynomial System in Two Ways
A Nice Polynomial System | Math Olympiads
Solving A Nice Polynomial Equation
A Cool Polynomial System | Nice Graph!
Комментарии
 0:09:03
0:09:03
 0:08:38
0:08:38
 0:09:27
0:09:27
 0:08:57
0:08:57
 0:10:56
0:10:56
 0:09:25
0:09:25
 0:10:27
0:10:27
 0:08:40
0:08:40
 0:30:09
0:30:09
 0:08:13
0:08:13
 0:06:23
0:06:23
 0:08:19
0:08:19
 0:11:06
0:11:06
 0:05:53
0:05:53
 0:10:27
0:10:27
 0:10:31
0:10:31
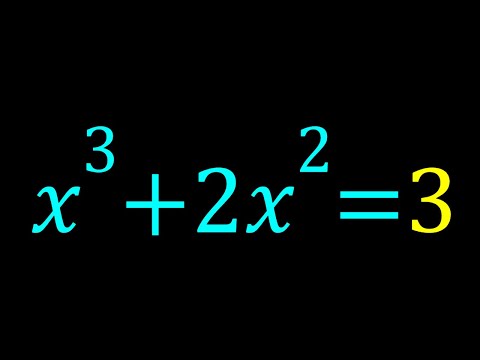 0:10:00
0:10:00
 0:10:49
0:10:49
 0:09:33
0:09:33
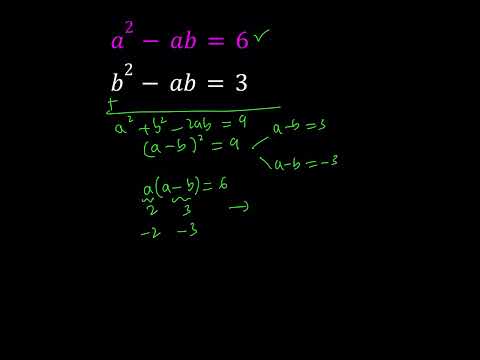 0:00:53
0:00:53
 0:10:59
0:10:59
 0:07:10
0:07:10
 0:08:35
0:08:35
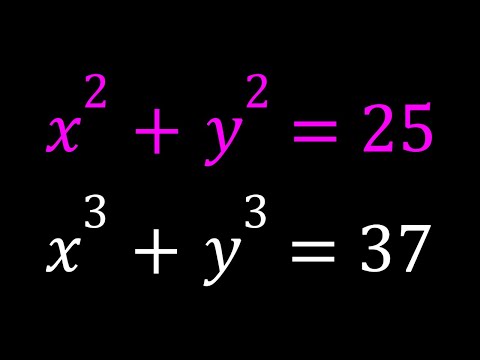 0:11:19
0:11:19