filmov
tv
Solving A Homemade Diophantine Equation

Показать описание
If you need to post a picture of your solution or idea:
#DiophantineEquations #NumberTheoryProblems
PLAYLISTS 🎵 :
#DiophantineEquations #NumberTheoryProblems
PLAYLISTS 🎵 :
Solving A Homemade Diophantine Equation
A Homemade Diophantine Equation | Integers
Solving a Diophantine Equation by Factoring | Solve for Integer Solutions #NumberTheory
A Quick and Easy Linear Diophantine System
Solving a Nice Diophantine Equation in Three Ways
Solving a Homemade Functional Equation in Two Ways
Solving A Nice Diophantine Equation from Romania
A Quick and Easy Diophantine Equation
A Nice Number Theory Math Olympiad Problem || Diophantine Equation || How to Solve @TheMathScholar23
Solving A Homemade Exponential Equation
One fairly easy diophantine equation anyone can solve | mathematica
Can You Find Integer Solutions? | Diophantine Equations | Math Olympiad Training
Solving a Cool Diophantine Equation: a^2+a+34=b^2
Diophantine Equations in Sudoku
A Diophantine Equation With Radicals
I Solved A Homemade Functional Equation
Solving a Quick and Easy Homemade Functional Equation
A Nice Homemade Exponential Equation
Let's Solve A Quick And EZ Diophantine Equation
I Solved A Homemade Functional Equation
A system of diophantine equations | feat. Fermat's Last Theorem | must watch till the end
A Quick and Easy Diophantine Equation | Primes
A Radical Idea: Solving A Homemade Radical System
Solving A Homemade Exponential Equation
Комментарии
 0:08:40
0:08:40
 0:08:38
0:08:38
 0:07:08
0:07:08
 0:10:57
0:10:57
 0:08:13
0:08:13
 0:10:26
0:10:26
 0:09:09
0:09:09
 0:02:20
0:02:20
 0:03:36
0:03:36
 0:08:46
0:08:46
 0:03:30
0:03:30
 0:01:54
0:01:54
 0:05:17
0:05:17
 0:58:26
0:58:26
 0:09:25
0:09:25
 0:09:39
0:09:39
 0:05:21
0:05:21
 0:05:31
0:05:31
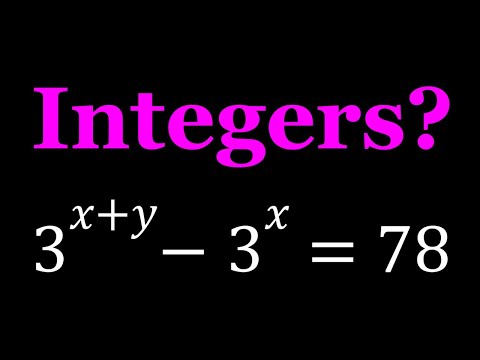 0:08:14
0:08:14
 0:09:50
0:09:50
 0:02:25
0:02:25
 0:05:37
0:05:37
 0:05:36
0:05:36
 0:09:01
0:09:01