filmov
tv
Evaluating A Septic Algebraic Expression

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #AlgebraicExpressions
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
Solving a Heptic Equation Without Using the Heptic Formula:
LECTURE:
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #AlgebraicExpressions
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
Solving a Heptic Equation Without Using the Heptic Formula:
LECTURE:
PLAYLISTS 🎵 :
Evaluating A Septic Algebraic Expression
Evaluating a Septic Algebraic Expression in Three Ways
Evaluating a Septic Algebraic Expression | A problem of algebra | if x+1/x=1 then find x^7+1/x^7
Evaluating An Algebraic Expression | Quadratics
Evaluating an Algebraic Expression in Terms of a
Evaluating an Algebraic Expression Using a Polynomial
Simple Way to Solve the Septic Polynomial Equation 16x^7+7x^3+1=0
Evaluating an Algebraic Expression from a Radical Equation
Factoring a septic polynomial. A challenge in algebra
Evaluating A Logarithmic Expression
Simplifying an Algebraic Expression (3 Ways)
Evaluating a Logarithmic Expression in Three Ways
Evaluating an Algebraic Expression for x+y+z=0
5 simple unsolvable equations
Let's Solve A Special Septic Equation | Polynomials
Evaluating a Logarithmic Expression from Another One
Evaluating A Homemade Function in Two Ways
Evaluating A Heptic Polynomial
Solving a very radical equation using a non-standard method. An algebraic challenge...
Simplifying A Radical | Math Olympiads
Simplifying a Cool Algebraic Expression in Two Ways
Solving a Nice Cubic System in Two Ways
A Polynomial System Inspired by Saratov Math Olympiads
A Nice Diophantine Equation
Комментарии
 0:09:14
0:09:14
 0:10:48
0:10:48
 0:03:35
0:03:35
 0:05:43
0:05:43
 0:10:03
0:10:03
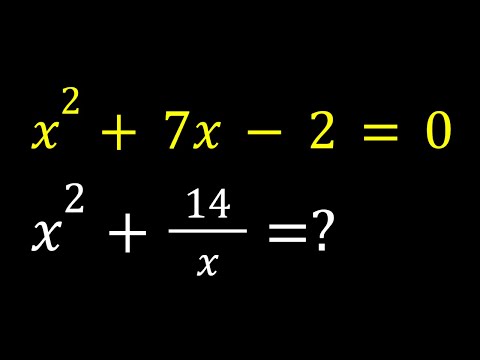 0:08:35
0:08:35
 0:02:12
0:02:12
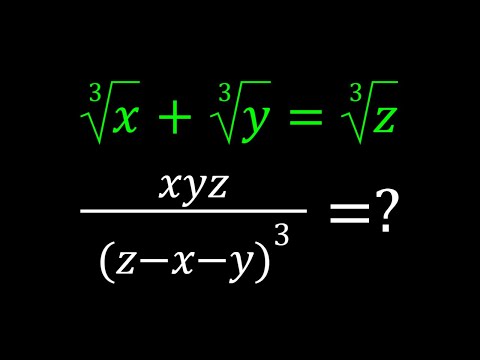 0:06:53
0:06:53
 0:09:43
0:09:43
 0:07:47
0:07:47
 0:05:42
0:05:42
 0:09:31
0:09:31
 0:13:47
0:13:47
 0:00:50
0:00:50
 0:08:57
0:08:57
 0:05:12
0:05:12
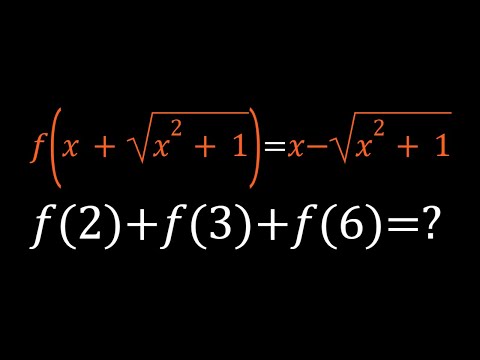 0:08:24
0:08:24
 0:10:08
0:10:08
 0:06:54
0:06:54
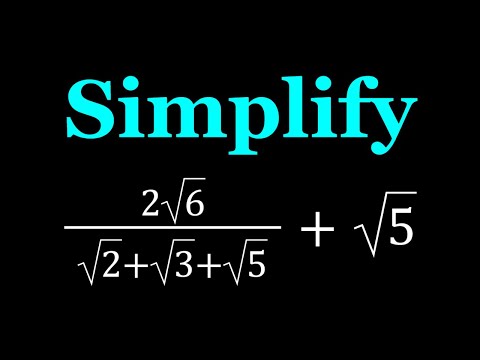 0:08:16
0:08:16
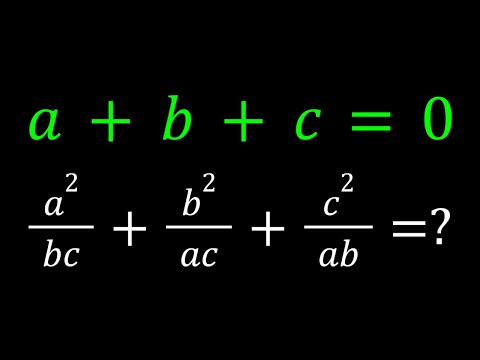 0:08:43
0:08:43
 0:09:13
0:09:13
 0:09:04
0:09:04
 0:08:56
0:08:56