filmov
tv
A Special Nonic Equation | Math Olympiads

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #PolynomialEquations #Polynomials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #PolynomialEquations #Polynomials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
A Special Nonic Equation Solved with a Special Method
A Special Nonic Equation | Math Olympiads
Solving a nonic equation using a non-standard method...An algebra challenge...
A nonic equation with a radical
Solving A Nonic Equation Using An Interesting Method
A Nonic Polynomial Equation
Solving a nonic equation from Indian Math challenge
Algebraic Equations: An Interesting Challenge Awaits!
A Linear Diophantine Equation
Let's Solve A Nonic Equation
A Special Quartic Equation | No Quartic Formula
How to Write Equation of High Degree Nonic Polynomial From Graph
Nonic Polynomial Function -- Find Equation From Graph
A non-standard quartic equation
A radical equation solved by using an ingenious method
A Special Cubic Equation
Solving a Non-Standard Equation For Reals
A Nice Polynomial System
Crack the Algebra Test in Math Olympiad
A Nice Rational Equation | Two Methods
Steps to Sketch a Nonic Polynomial
Solving a Nice Polynomial Equation
A challenging rational equation
Solving a Diophantine Equation for Rational Solutions
Комментарии
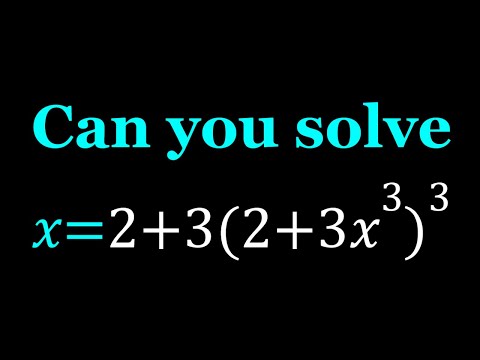 0:10:04
0:10:04
 0:09:44
0:09:44
 0:07:08
0:07:08
 0:14:37
0:14:37
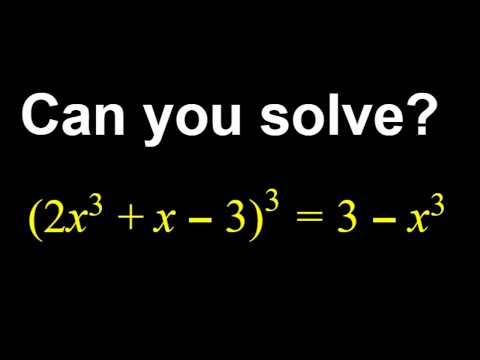 0:07:08
0:07:08
 0:08:12
0:08:12
 0:09:35
0:09:35
 0:12:56
0:12:56
 0:00:27
0:00:27
 0:09:13
0:09:13
 0:05:52
0:05:52
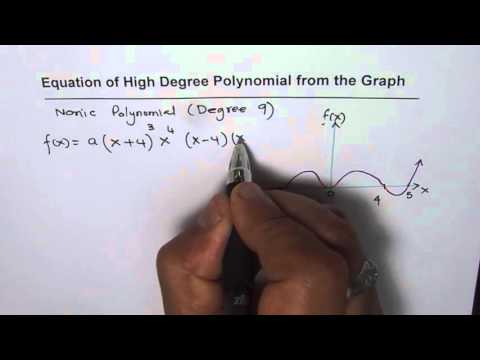 0:09:07
0:09:07
 0:06:36
0:06:36
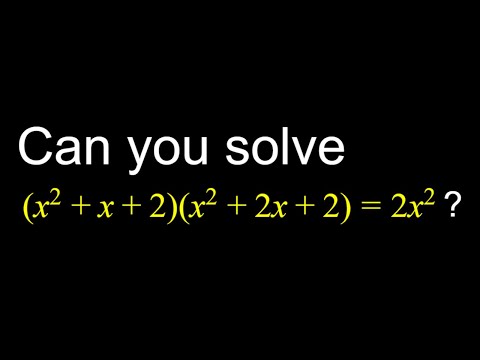 0:06:09
0:06:09
 0:07:28
0:07:28
 0:08:17
0:08:17
 0:04:34
0:04:34
 0:08:40
0:08:40
 0:09:55
0:09:55
 0:09:24
0:09:24
 0:08:19
0:08:19
 0:05:53
0:05:53
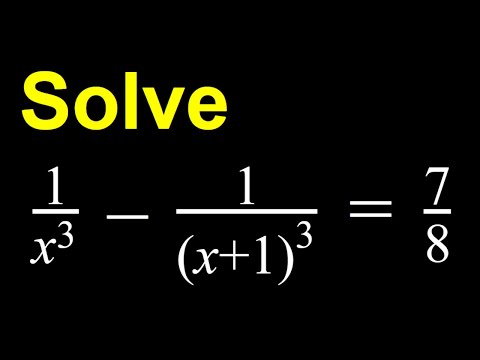 0:13:14
0:13:14
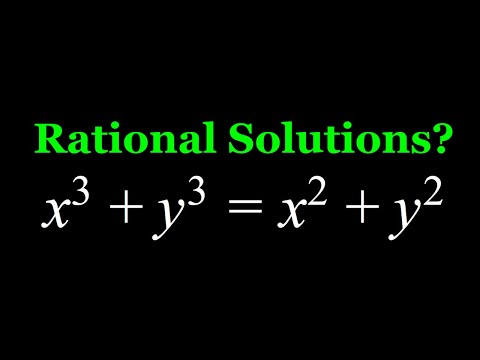 0:07:31
0:07:31