filmov
tv
A Homemade Polynomial System Solved in Two Ways
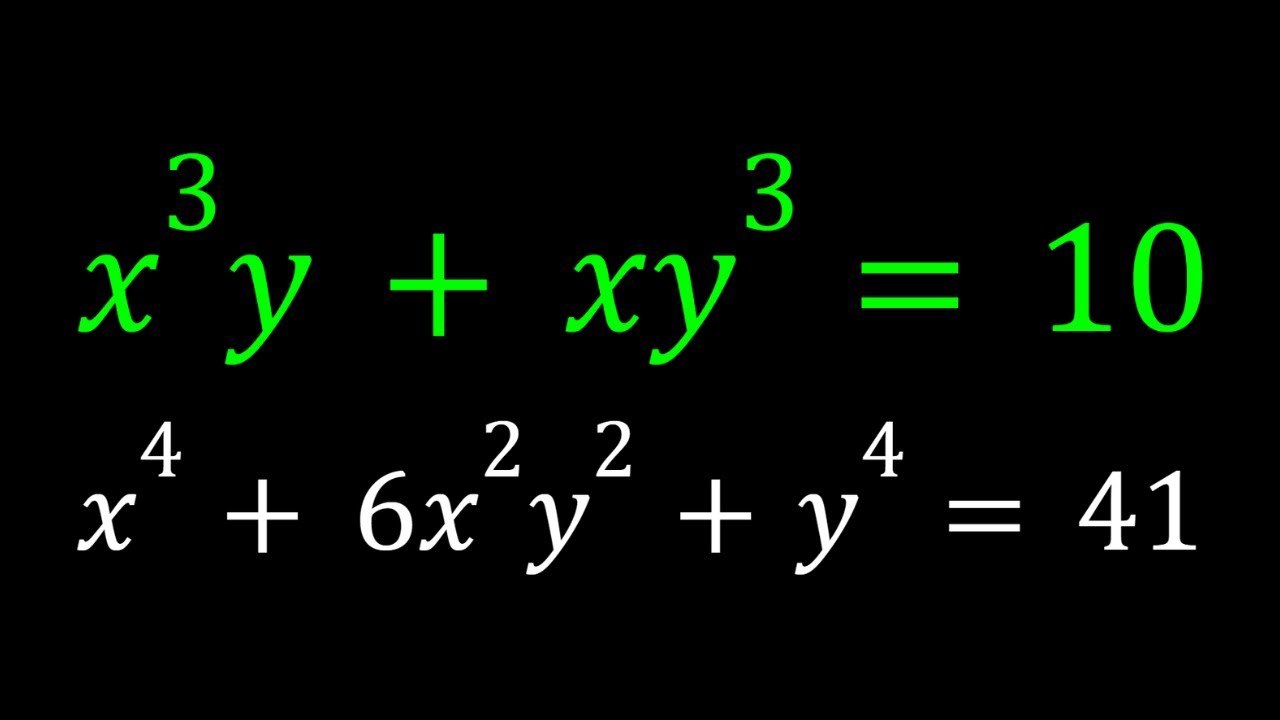
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #PolynomialEquations #PolynomialSystems
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
#ChallengingMathProblems #PolynomialEquations #PolynomialSystems
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
A Homemade Polynomial System Solved in Two Ways
Solving a Homemade Polynomial System
Solving a Homemade Polynomial Equation
Solving a Nice Polynomial System in Two Ways
Solving a Nice Polynomial System in Two Ways
Solving a Nice Polynomial System in Two Ways
Solving A Nice Polynomial System | Two Ways
xavier memes #memes
A case that shocked Canada in 2012😳 #shorts
NEWYES Calculator VS Casio calculator
Last Words of Albert Einstein #shorts
I Made Up A Polynomial System
A Nice Polynomial System Solved in Three Ways
Solving A Nice Polynomial System | Algebra
A Nice Polynomial System
Solving polynomial systems --- CAG L19
A Polynomial System Inspired by Saratov Math Olympiads
A Nice, Quick, and Easy Polynomial System
Japanese Method #shorts
Solving A Polynomial System
ILLEGAL Move & WIN the Game! #shorts
Completing the square using algebra tiles - Demo
Polynomial System with Two Equations and Three Variables
Can You Solve this Polynomial Equation? | Fast & Easy Tutorial
Комментарии
 0:11:56
0:11:56
 0:14:25
0:14:25
 0:07:08
0:07:08
 0:09:03
0:09:03
 0:09:27
0:09:27
 0:08:38
0:08:38
 0:10:56
0:10:56
 0:00:06
0:00:06
 0:00:14
0:00:14
 0:00:14
0:00:14
 0:00:37
0:00:37
 0:08:53
0:08:53
 0:09:33
0:09:33
 0:08:57
0:08:57
 0:11:00
0:11:00
 0:28:17
0:28:17
 0:09:04
0:09:04
 0:08:27
0:08:27
 0:00:20
0:00:20
 0:03:11
0:03:11
 0:00:35
0:00:35
 0:02:24
0:02:24
 0:08:29
0:08:29
 0:09:04
0:09:04