filmov
tv
Solving x^3+x-10=0 in Two Ways
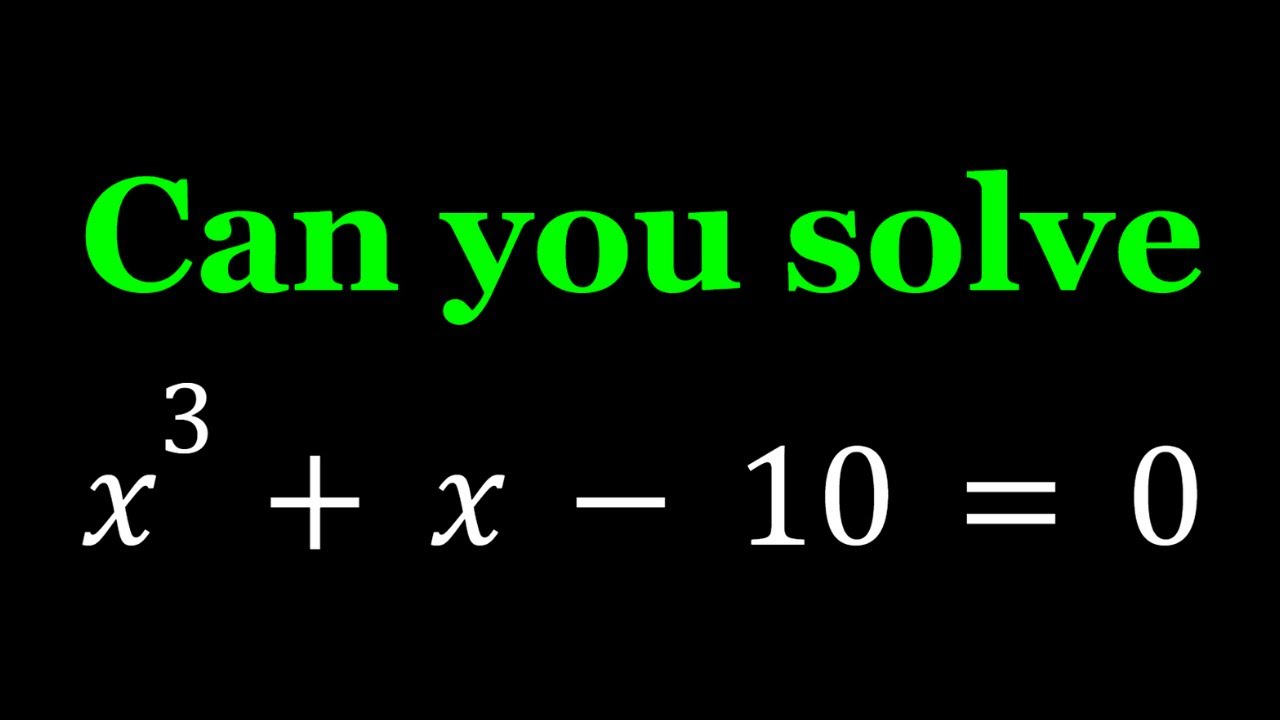
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #PolynomialEquations
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
#ChallengingMathProblems #PolynomialEquations
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
Solving x^3+x-10=0 in Two Ways
5 simple unsolvable equations
Solve by completing the square x^2+3x-10=0
How to Solve x^2 + 3x -10 = 0 by Factoring
How to Solve x^2 - 3x - 10 = 0 by Factoring
Solving an equation with variables on both side and one solution
Solve by completing the square | Step by Step Technique
Solve quadratic equation by factorisation
Quadratic Equation: Solve x^2 - 3x - 10 = 0
Solve by Completing the Square: Step-by-Step Technique
Factorising cubic functions: The kx method
Solving a quadratic by completing the square
Solve by Completing the Square x^2+10x-3=0
Solving using the quadratic formula with complex solutions
Solving Quadratic Equations using Quadratic Formula - Quadratic Equations
Solve an exponential equation by taking log of both sides & approximating the value
Solve x²+3x-10=0 by factorization
Solve Quadratic Equations By Factoring - Simple Trick No Fuss!
Method of Elimination Steps to Solve Simultaneous Equations
How to Solve Quadratic Equations by Completing the Square? Grade 9 Math
x2-3x-10=0 Factorisation | Find the Roots of the Quadratic Equations by Factorisation x2-3x-10=0
Solving x^3+x^2+4=0 in Two Ways
How To Solve Absolute Value Equations, Basic Introduction, Algebra
Exponential Equations - Algebra and Precalculus
Комментарии
 0:06:33
0:06:33
 0:00:50
0:00:50
 0:02:37
0:02:37
 0:02:09
0:02:09
 0:02:19
0:02:19
 0:02:36
0:02:36
 0:05:20
0:05:20
 0:09:05
0:09:05
 0:01:28
0:01:28
 0:07:40
0:07:40
 0:10:22
0:10:22
 0:10:43
0:10:43
 0:02:34
0:02:34
 0:05:28
0:05:28
 0:09:06
0:09:06
 0:03:23
0:03:23
 0:02:58
0:02:58
 0:06:31
0:06:31
 0:02:58
0:02:58
 0:06:32
0:06:32
 0:01:40
0:01:40
 0:10:27
0:10:27
 0:04:21
0:04:21
 0:05:58
0:05:58