filmov
tv
Solving a Radical Exponential Equation
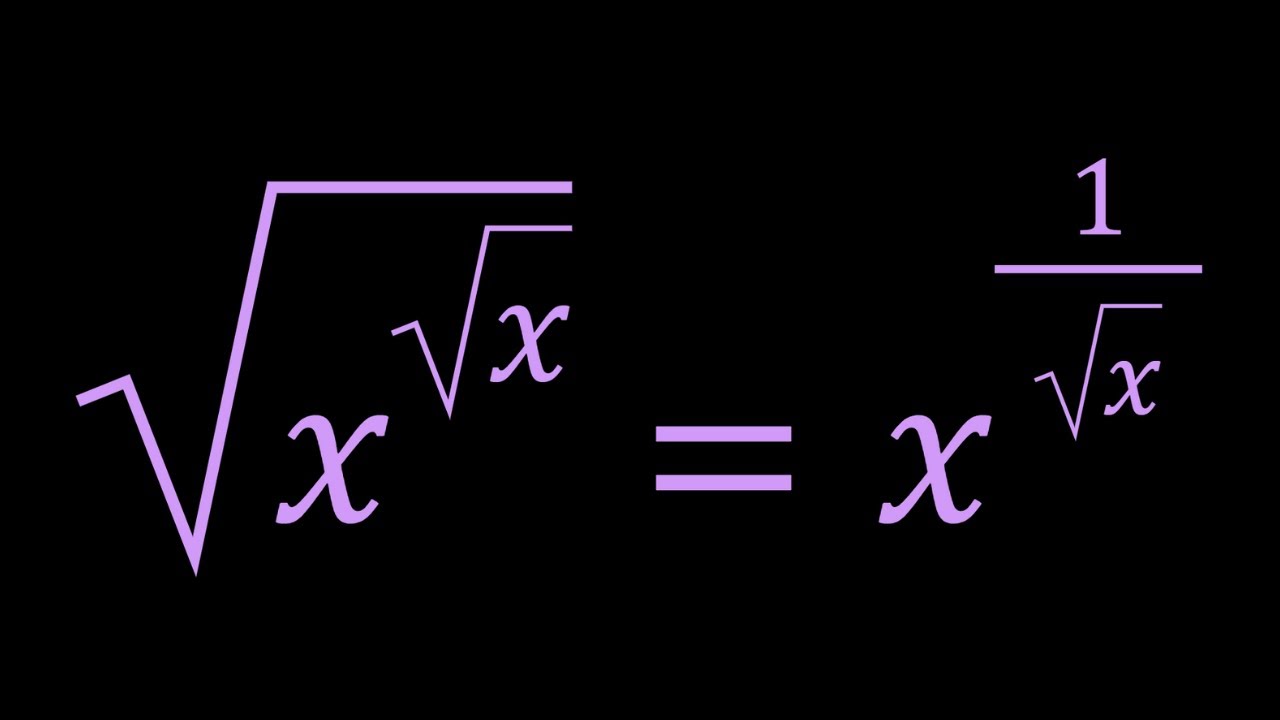
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #Radicals #RadicalEquations #ExponentialEquations
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
#ChallengingMathProblems #Radicals #RadicalEquations #ExponentialEquations
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
Solving radical equations | Exponent expressions and equations | Algebra I | Khan Academy
Math Problems - Exponential Equations With Radicals
Solving Radical Equations
Solving Exponential Equations
Solving a Radical Exponential Equation
A Radical Exponential Equation
Solving a Radical Exponential Equation
How to solve a radical equation by using rational powers using absolute value
A Nice Square Root Simplification Math Problem. #shorts #maths #radical #squareroot #olympiad
A Radical Exponential Equation with Square Roots
Solving A Radical Exponential Equation
Exponential Equations - Algebra and Precalculus
How To Convert Between Exponential Form and Radical Form - Algebra
Solving A Radical Exponential Equation
Fractional Exponents
How I Solved A Radical Exponential Equation For All Solutions
Solving A Radical Exponential Equation
15 Solve Exponential Equation with Radicals
Solving radical equations 1 | Exponent expressions and equations | Algebra I | Khan Academy
Solving Exponential Equation
How to solve an equation with fraction powers in your exponent
Solving radical equations 2 | Exponent expressions and equations | Algebra I | Khan Academy
Can you solve this? | Exponential Equation | Algebra Problem.
How to Solve an Interesting Radical Exponential Equation. Step-by-Step Solutions | Math Olympiad
Комментарии
 0:03:11
0:03:11
 0:06:55
0:06:55
 0:17:11
0:17:11
 0:16:36
0:16:36
 0:10:23
0:10:23
 0:08:31
0:08:31
 0:05:05
0:05:05
 0:07:38
0:07:38
 0:00:47
0:00:47
 0:06:51
0:06:51
 0:00:36
0:00:36
 0:05:58
0:05:58
 0:14:19
0:14:19
 0:11:58
0:11:58
 0:11:32
0:11:32
 0:09:29
0:09:29
 0:00:36
0:00:36
 0:03:11
0:03:11
 0:02:15
0:02:15
 0:00:56
0:00:56
 0:03:47
0:03:47
 0:03:34
0:03:34
 0:03:33
0:03:33
 0:10:04
0:10:04