filmov
tv
Solving a Functional Equation by Elimination
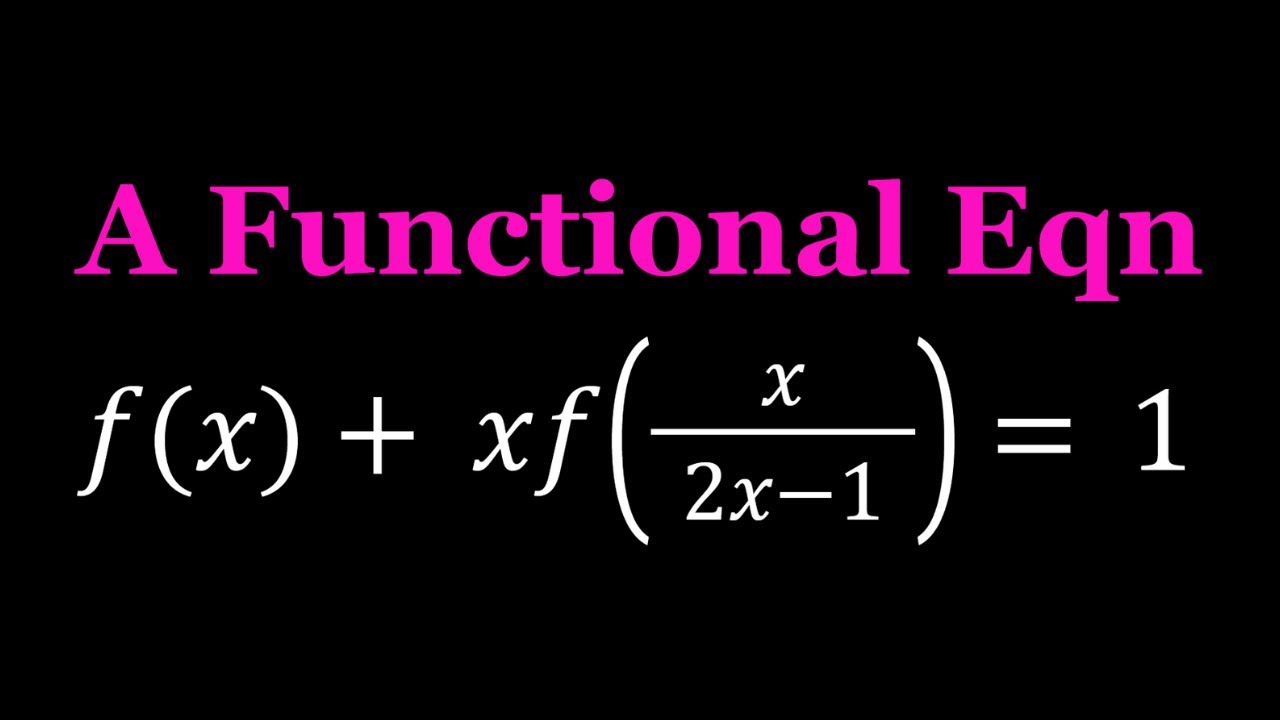
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FunctionalEquations
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
#ChallengingMathProblems #FunctionalEquations
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
A Quick and Easy Functional Equation
A Nice and Easy Functional Equation
Solving a Functional Equation
Solving a Quick and Easy Functional Equation
Solving a Functional Equation
the greatest functional equation of all time.
A Functional Equation from Samara Math Olympiads
Let's Solve A Functional Equation
An Interesting Functional Equation | ioqm | algebra questions | how to solve maths problems quickly
Solving A Functional System of Equations in Two Ways
Solving a Quick and Easy Functional Equation
Algebra Solving a Functional Equation Example
Solving a Functional Equation by Elimination
Solving A Functional Equation
A Functional Equation from Putnam and Beyond
Solving a Rational Functional Equation
A Functional Equation from British Math Olympiads 2009
Solving A Nice Functional Equation
Balkan Math Olympiad 2000 - Problem 1: A classic functional equation
Solving the functional equation f[x+f(y)]=x+y+1
a functional equation /functional equation
A Curious Functional Equation | Math Olympiads
Gaining Insights: Solving a Functional Equation
Solving the Functional Equation f(x+y)=f(x)f(y)
Комментарии
 0:06:49
0:06:49
 0:05:07
0:05:07
 0:10:36
0:10:36
 0:05:47
0:05:47
 0:10:36
0:10:36
 0:07:48
0:07:48
 0:08:47
0:08:47
 0:08:55
0:08:55
 0:13:08
0:13:08
 0:09:27
0:09:27
 0:06:19
0:06:19
 0:01:37
0:01:37
 0:09:08
0:09:08
 0:11:58
0:11:58
 0:12:07
0:12:07
 0:06:53
0:06:53
 0:08:33
0:08:33
 0:09:50
0:09:50
 0:13:58
0:13:58
 0:06:01
0:06:01
 0:04:42
0:04:42
 0:08:29
0:08:29
 0:10:22
0:10:22
 0:10:18
0:10:18