filmov
tv
Solving for An Algebraic Expression in Two Ways

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #AlgebraicExpressions
EXPLORE 😎:
PLAYLISTS 🎵 :
#ChallengingMathProblems #AlgebraicExpressions
EXPLORE 😎:
PLAYLISTS 🎵 :
How to Simplify an Expression: A Beginner's Guide | Algebraic Expressions | Math with Mr. J
Algebra Basics: Solving 2-Step Equations - Math Antics
Algebraic Expressions (Basics)
Algebra - How To Solve Equations Quickly!
Simplify Grade 10 Algebraic Expressions
Intro to Evaluating Algebraic Expressions | How to Evaluate Algebraic Expressions | Math with Mr. J
GCSE Maths - How to Solve Algebraic Equations (Part 1 of 3) #43
Solving Two-Step Equations | Algebra Equations
#maths | A Beautiful Radical Equation | Algebra Challenge #algebra #allpracticalofficial
Simplify Algebraic Expressions: a(x+b)-c(x-d)
Writing Algebraic Expressions | Writing Expressions with Variables | Math with Mr. J
Solving an equation with variables on both side and one solution
Algebraic Expressions – Algebra Basics
ALGEBRAIC EXPRESSIONS & EQUATIONS | GRADE 6
What are variables, expressions, and equations? | Introduction to algebra | Algebra I | Khan Academy
How To Evaluate Algebraic Expressions
Solving Two-Step Equations | Expressions & Equations | Grade 7
Learn How To Solve Equations – Understand In 7 Minutes
Algebraic Word Problems
How to Solve One-Step Equations | One-Step Equation Steps | Math with Mr. J
Solve the equation
SOLVING ALGEBRAIC EQUATIONS | GRADE 6
Translating Words To Algebraic Expressions Explained!
Algebra Basics: Solving Basic Equations Part 1 - Math Antics
Комментарии
 0:55:18
0:55:18
 0:10:29
0:10:29
 0:09:56
0:09:56
 0:25:05
0:25:05
 0:07:45
0:07:45
 0:05:32
0:05:32
 0:06:13
0:06:13
 0:09:13
0:09:13
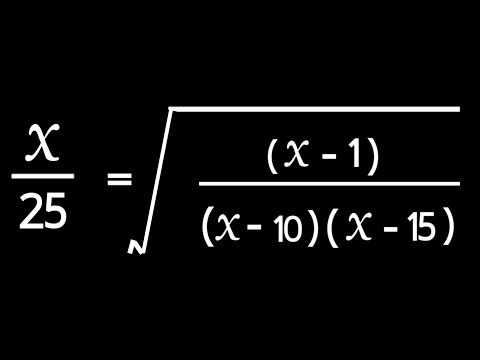 0:16:28
0:16:28
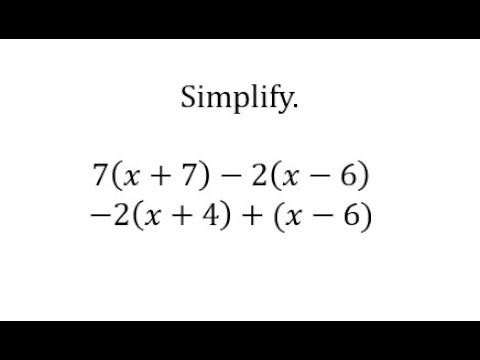 0:02:46
0:02:46
 0:12:52
0:12:52
 0:02:36
0:02:36
 0:14:41
0:14:41
 0:20:45
0:20:45
 0:06:55
0:06:55
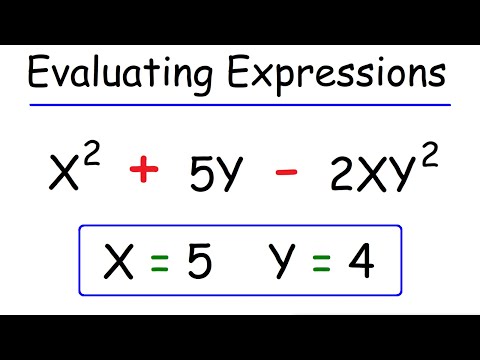 0:13:55
0:13:55
 0:03:40
0:03:40
 0:12:34
0:12:34
 0:05:38
0:05:38
 0:06:54
0:06:54
 0:01:53
0:01:53
 0:18:35
0:18:35
 0:10:43
0:10:43
 0:11:08
0:11:08