filmov
tv
Solving f(xy)=xf(y) in Two Ways
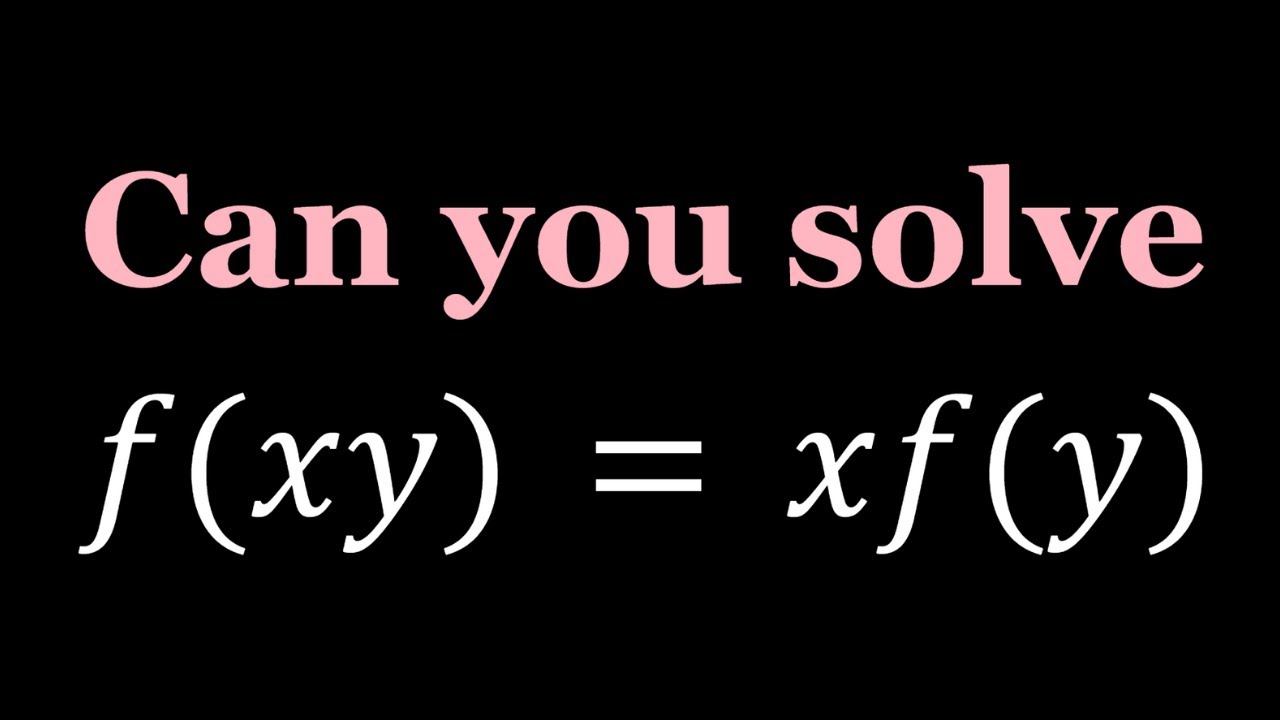
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FunctionalEquations
PLAYLISTS 🎵 :
#ChallengingMathProblems #FunctionalEquations
PLAYLISTS 🎵 :
Solving f(xy)=xf(y) in Two Ways
Solving f(x+y)=f(x)+f(y)+2xy in Two Ways
Solving the Functional Equation f(x-y)=f(x)f(y)
Solving the Functional Equation f(xy+1)=xf(y)-f(x)+6
A Functional Equation | f(xy)=xf(y)+yf(x)
Solving the Functional Equation f(x+y)=f(x)f(y)
Solving f(x-f(y))=1-x-y
A Functional Equation f(x+y)=f(x)+f(y)-xy
Solving the Functional Equation f(x+y)=xf(y)
Solving the Functional Equation f(f(x)+y)=x/(1+xy)
Solving the Functional Equation f(x - y) = f(x) - f(y)
Solving f(x)=yf(xy) in Two/Three Ways
A Nice Functional Equation [f(x+y)=f(x)+f(y)+2xy]
f(x+y) = f(x)f(y)
Solving a Homemade Functional Equation in Two Ways
A Quick and Easy Functional Equation
Solving A Functional System of Equations in Two Ways
A Rational Functional Equation Solved in Two Ways
Solving Two Functional Equations
Evaluating f(xy)=f(x)+f(y)-1
solving y.f(x) = x.f(y) | solve for f(x)....!
Solving a Non-standard System of Equations
Total Differential of Multivariate Function f(x, y) = x^3y^4 + x^2y^3 + 12
Multiplicative Functional Equation
Комментарии
 0:03:27
0:03:27
 0:09:14
0:09:14
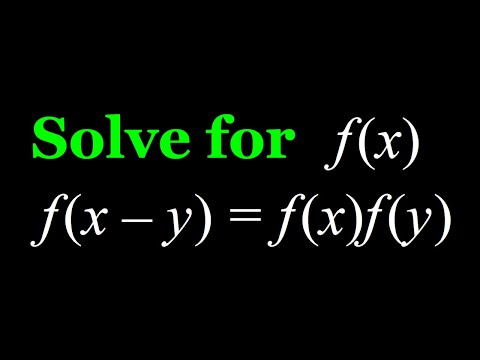 0:05:41
0:05:41
 0:05:51
0:05:51
 0:08:58
0:08:58
 0:10:18
0:10:18
 0:06:56
0:06:56
 0:07:54
0:07:54
 0:06:11
0:06:11
 0:05:51
0:05:51
 0:06:21
0:06:21
 0:08:37
0:08:37
 0:12:10
0:12:10
 0:07:14
0:07:14
 0:10:26
0:10:26
 0:06:49
0:06:49
 0:09:27
0:09:27
 0:08:51
0:08:51
 0:08:50
0:08:50
 0:04:41
0:04:41
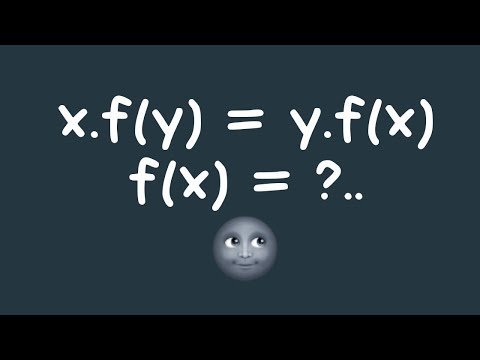 0:03:14
0:03:14
 0:10:17
0:10:17
 0:01:59
0:01:59
 0:17:42
0:17:42