filmov
tv
Solving a Homemade Functional Equation in Two Ways

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #Functions #FunctionalEquations
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
#ChallengingMathProblems #Functions #FunctionalEquations
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
Solving a Homemade Functional Equation in Two Ways
Solving A Homemade Functional Equation
Solving a Homemade Functional Equation 1
Solving a Quick and Easy Homemade Functional Equation
Let's Solve A Homemade Functional Equation
I Solved A Homemade Functional Equation
I Solved A Homemade Functional Equation
A Nice Homemade Functional Equation
Solving a Quick and Easy Functional Equation
I Solved A Homemade Functional Equation in Two Ways
A Homemade Functional Equation | Math Olympiads
A Homemade Functional Equation with Natural Log
A Homemade Functional Equation
Solving a Quick and Easy Functional Equation
Have You Solved a Functional Equation Before?
I Made A Functional Equation 😊
Solving a Functional Equation
Let's Solve A Functional Equation
A Homemade Functional Equation | Two Solutions?
A Homemade Functional Equation | Bonus at the End
A Nice Homemade Functional Equation
Solving A Nice Functional Equation
A Quick and Easy Functional Equation from Slovenia
a functional equation /functional equation
Комментарии
 0:10:26
0:10:26
 0:08:44
0:08:44
 0:08:55
0:08:55
 0:05:21
0:05:21
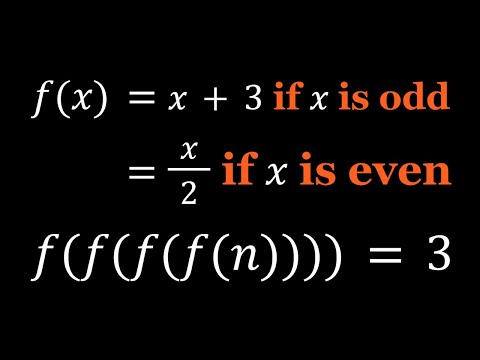 0:08:41
0:08:41
 0:09:39
0:09:39
 0:09:50
0:09:50
 0:09:22
0:09:22
 0:06:19
0:06:19
 0:08:57
0:08:57
 0:10:14
0:10:14
 0:09:18
0:09:18
 0:09:36
0:09:36
 0:08:18
0:08:18
 0:00:40
0:00:40
 0:10:54
0:10:54
 0:10:36
0:10:36
 0:08:55
0:08:55
 0:08:41
0:08:41
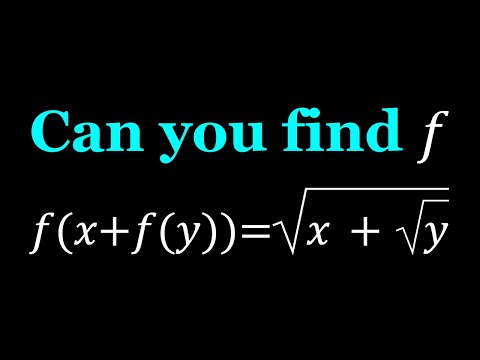 0:08:33
0:08:33
 0:08:21
0:08:21
 0:09:50
0:09:50
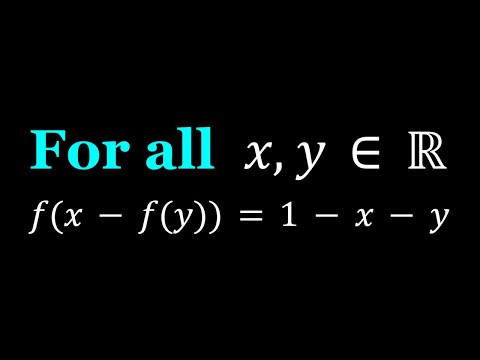 0:06:25
0:06:25
 0:04:42
0:04:42