filmov
tv
Solving the Functional Equation f(x-y)=f(x)f(y)
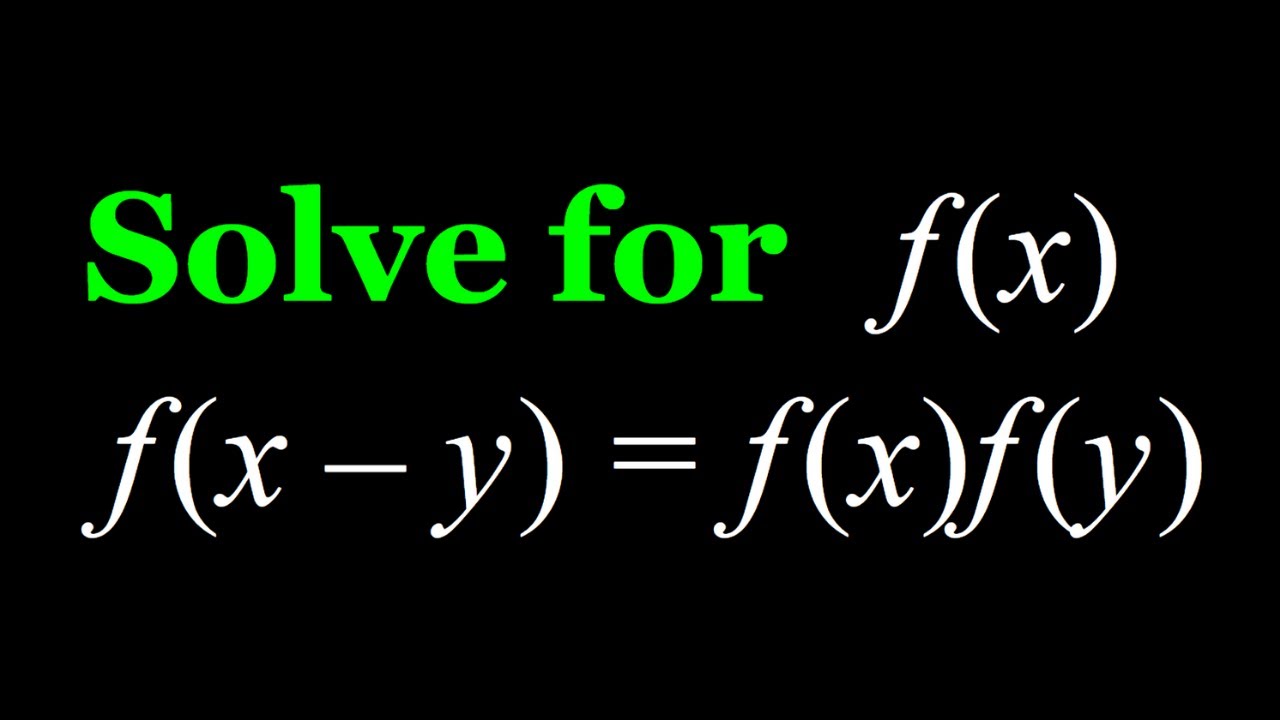
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FunctionalEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
#ChallengingMathProblems #FunctionalEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
Solving the Functional Equation f(x+y)=f(x)f(y)
Solving the Functional Equation f(x - y) = f(x) - f(y)
Solving The Functional Equation f(x-y) = f(x) - f(y)
Solving the Functional Equation f(xy+1)=xf(y)-f(x)+6
Solving the Functional Equation f(x-y)=f(x)f(y)
A Functional Equation f(x+y)=f(x)+f(y)-xy
Solving the functional equation f[x+f(y)]=x+y+1
f(x+y) = f(x)f(y)
Relations And Functions | Class 11 Maths | NCERT Solutions
How to solve the functional equation f(x+y)=f(x)+f(y) .
Solving f(sqrt(x^2+y^2))=f(x)f(y)
Solving the Functional Equation f(x+y)=xf(y)
Solving a Czech-Polish-Slovak Functional Equation || High School Math
Visualization of the solutions to the functional equation
Solving f(xy)=xf(y) in Two Ways
A Nice and Easy Functional Equation
What is the Jensen's Functional Equation?
Find the function f(x) in the Functional Equation | Try this simple Trick | Math Olympiad Training
Solving a Functional Equation | f(x)+f(x-1)=x^2
A Nice Functional Equation [f(x+y)=f(x)+f(y)+2xy]
Solving f(x/y)=f(x)/f(y), A Nice Functional Equation
Brain Recovery | Easy To Follow | Solving f(xy)=f(x)+f(y)
Evaluating f(xy)=f(x)+f(y)-1
Solving the Functional Equation f(f(x)+y)=x/(1+xy)
Комментарии
 0:10:18
0:10:18
 0:06:21
0:06:21
 0:03:02
0:03:02
 0:05:51
0:05:51
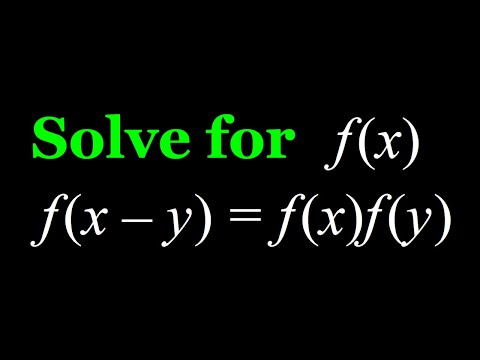 0:05:41
0:05:41
 0:07:54
0:07:54
 0:06:01
0:06:01
 0:07:14
0:07:14
 1:08:37
1:08:37
 0:11:18
0:11:18
 0:08:06
0:08:06
 0:06:11
0:06:11
 0:11:28
0:11:28
 0:11:35
0:11:35
 0:03:27
0:03:27
 0:05:07
0:05:07
 0:05:27
0:05:27
 0:04:47
0:04:47
 0:08:59
0:08:59
 0:12:10
0:12:10
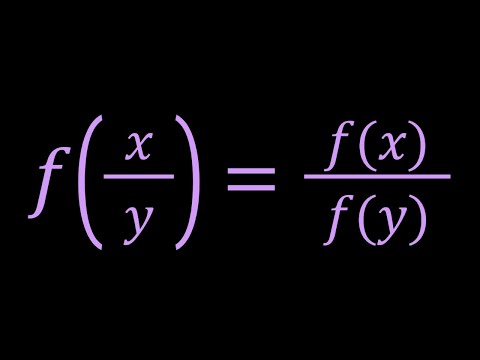 0:07:10
0:07:10
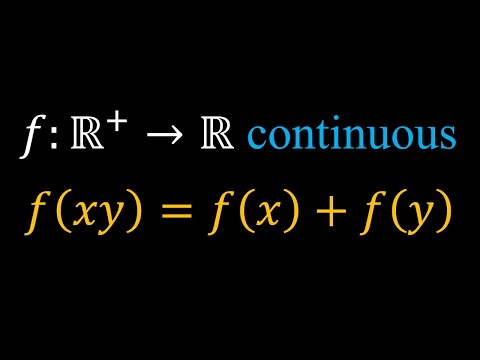 0:02:21
0:02:21
 0:04:41
0:04:41
 0:05:51
0:05:51