filmov
tv
A Functional Equation f(x+y)=f(x)+f(y)-xy
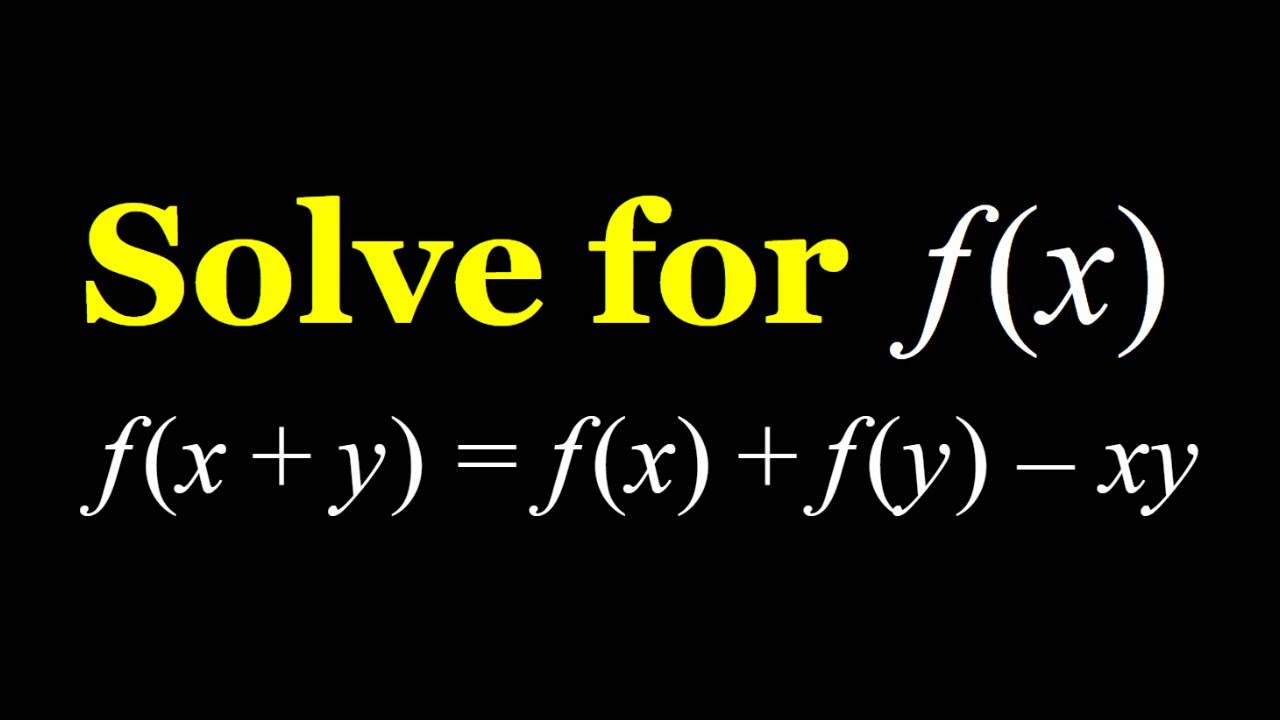
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FunctionalEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
#ChallengingMathProblems #FunctionalEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
Комментарии




















![Solving f(x)+f(y)=f[(x+y)/(1-xy)]](https://i.ytimg.com/vi/Xyl1M40zmbs/hqdefault.jpg)