filmov
tv
Evaluating f(xy)=f(x)+f(y)-1
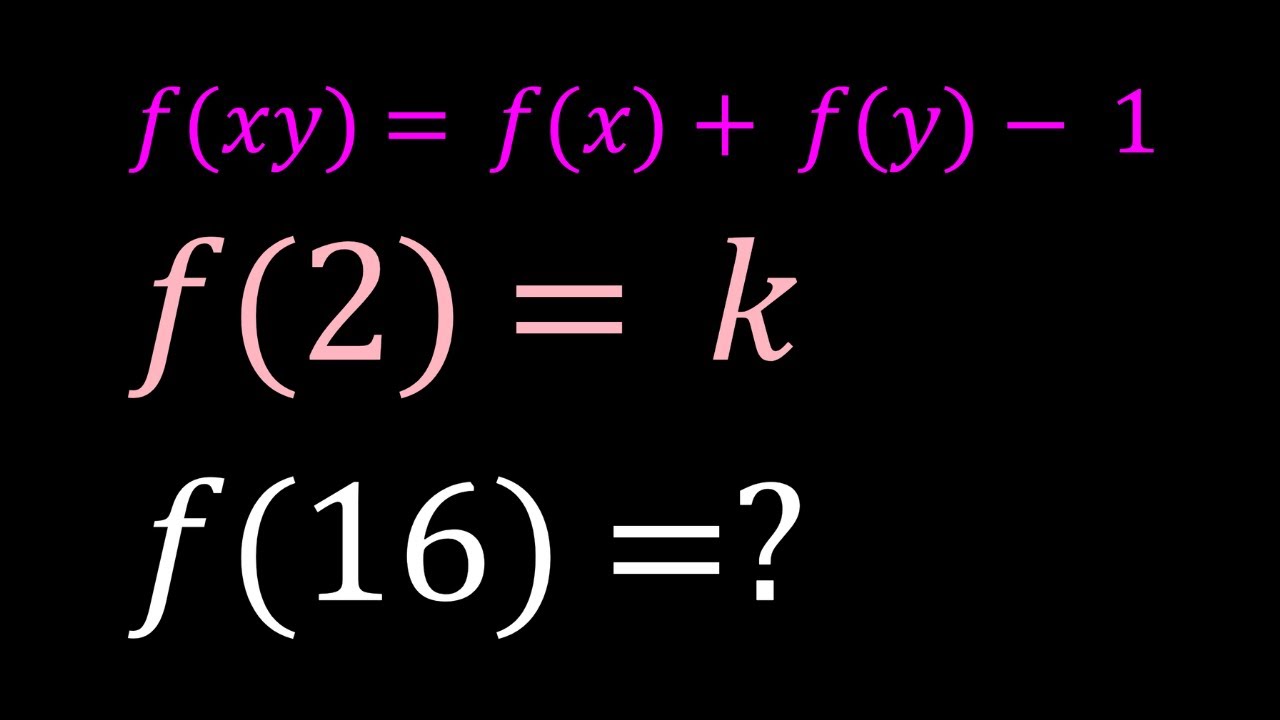
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FunctionalEquations #Functions
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
#ChallengingMathProblems #FunctionalEquations #Functions
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
Evaluating f(xy)=f(x)+f(y)-1
Solving the Functional Equation f(x-y)=f(x)f(y)
Solving the Functional Equation f(f(x)+y)=x/(1+xy)
Solving The Functional Equation f(x-y) = f(x) - f(y)
Learn how to evaluate for a function
Solving f(x-f(y))=1-x-y
No Need To Lose Brain Cells| Easiest Method | f(xy)=yf(x)+xf(y)
Partial Derivatives - Multivariable Calculus
Solving f(xy)=xf(y) in Two Ways
Solving f(xy)=f(x)-f(1/y)
Solving the Functional Equation f(xy+1)=xf(y)-f(x)+6
Brain Recovery | Easy To Follow | Solving f(xy)=f(x)+f(y)
A Functional Equation | f(xy)=xf(y)+yf(x)
Evaluate a Function from a Graph
Local Extrema, Critical Points, & Saddle Points of Multivariable Functions - Calculus 3
5 simple unsolvable equations
A Functional Equation f(x+y)=f(x)+f(y)-xy
Find the local maxima minima and saddle points of f(x y)=xy(1-x-y) Partial differentiation
Evaluate the indicated partial derivatives. f(x, y)=x^2 y e^x y ; ∂f / ∂x(1,1),…
First Order Partial Derivatives of f(x, y) = e^(xy)
Learn Functions – Understand In 7 Minutes
First Order Partial Derivatives of z = f(xy)
Total Differential of Multivariate Function f(x, y) = x^3y^4 + x^2y^3 + 12
Finding derivatives from a graph
Комментарии
 0:04:41
0:04:41
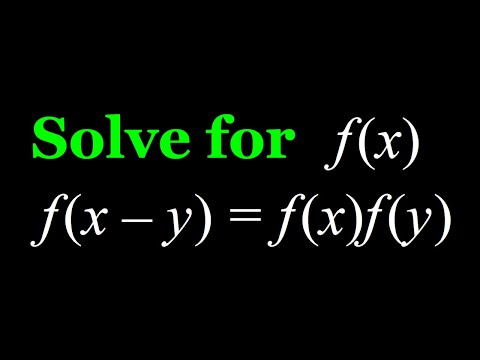 0:05:41
0:05:41
 0:05:51
0:05:51
 0:03:02
0:03:02
 0:02:15
0:02:15
 0:06:56
0:06:56
 0:02:57
0:02:57
 1:00:33
1:00:33
 0:03:27
0:03:27
 0:06:00
0:06:00
 0:05:51
0:05:51
 0:02:21
0:02:21
 0:08:58
0:08:58
 0:04:29
0:04:29
 0:14:35
0:14:35
 0:00:50
0:00:50
 0:07:54
0:07:54
 0:05:29
0:05:29
 0:00:33
0:00:33
 0:01:47
0:01:47
 0:09:43
0:09:43
 0:01:43
0:01:43
 0:01:59
0:01:59
 0:05:21
0:05:21