filmov
tv
Solving the Functional Equation f(f(x)+y)=x/(1+xy)

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FunctionalEquations #Functions
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
#ChallengingMathProblems #FunctionalEquations #Functions
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
Solving the Functional Equation f(f(x)+y)=x/(1+xy)
Solving f(x)+f(y)=f[(x+y)/(1-xy)]
Solving the Functional Equation f(xy+1)=xf(y)-f(x)+6
Solving the functional equation f[x+f(y)]=x+y+1
Solving the Functional Equation f(x+y)=f(x)f(y)
A Functional Equation f(x+y)=f(x)+f(y)-xy
Solving f(x-f(y))=1-x-y
Solving The Functional Equation f(x-y) = f(x) - f(y)
Relations And Functions | Class 11 Maths | NCERT Solutions
Solving the Functional Equation f(x-y)=f(x)f(y)
Solving the Functional Equation f(x - y) = f(x) - f(y)
Solving f(xy)=f(x)-f(1/y)
5 simple unsolvable equations
A Functional Equation | f(xy)=xf(y)+yf(x)
Solving a Functional Equation
Solving the Functional Equation f(x+y)=xf(y)
A Quick and Easy Functional Equation
International Math Olympiad 2010 Problem 1 - A beautiful functional equation from the IMO
That's Why Mohit Sir Called 'God Of Mathematics'| Puzzle Brain teaser | #competishun ...
Solving an equation for y and x
Solving f((2x-1)/2)=x^2-x, a Functional Equation
Solving a Quick and Easy Homemade Functional Equation
Functional Equation f(x+y) = f(x) + f(y) -2xy -1 (By PK SIR IIT BHU ) || IIT JEE Mathematics
How REAL Men Integrate Functions
Комментарии
 0:05:51
0:05:51
![Solving f(x)+f(y)=f[(x+y)/(1-xy)]](https://i.ytimg.com/vi/Xyl1M40zmbs/hqdefault.jpg) 0:14:09
0:14:09
 0:05:51
0:05:51
 0:06:01
0:06:01
 0:10:18
0:10:18
 0:07:54
0:07:54
 0:06:56
0:06:56
 0:03:02
0:03:02
 1:08:37
1:08:37
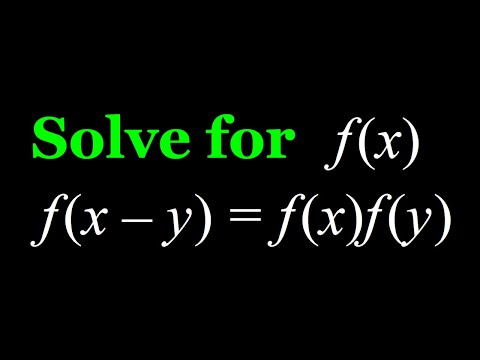 0:05:41
0:05:41
 0:06:21
0:06:21
 0:06:00
0:06:00
 0:00:50
0:00:50
 0:08:58
0:08:58
 0:10:36
0:10:36
 0:06:11
0:06:11
 0:06:49
0:06:49
 0:13:47
0:13:47
 0:00:19
0:00:19
 0:03:47
0:03:47
 0:05:38
0:05:38
 0:05:21
0:05:21
 0:08:29
0:08:29
 0:00:35
0:00:35