filmov
tv
A Rational Functional Equation Solved in Two Ways
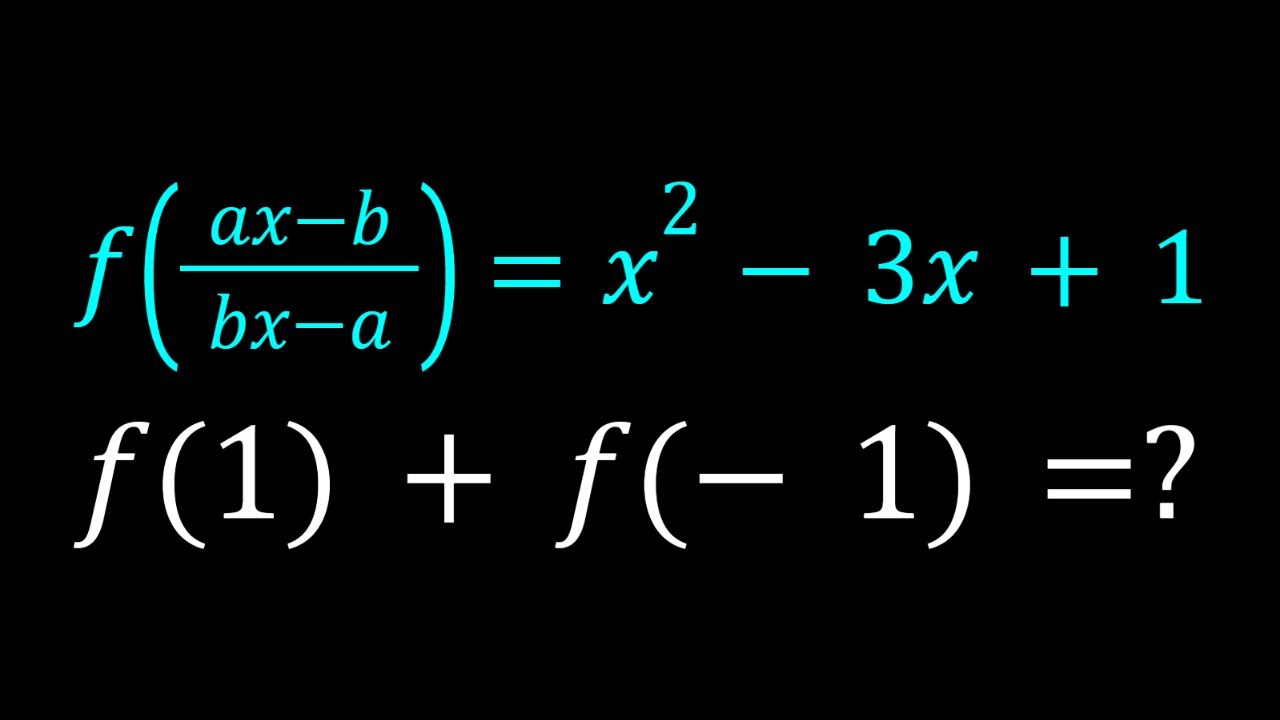
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FunctionalEquations
PLAYLISTS 🎵 :
#ChallengingMathProblems #FunctionalEquations
PLAYLISTS 🎵 :
Solving a Rational Functional Equation
Solving Rational Equations
A Rational Functional Equation Solved in Two Ways
A Nice and Easy Functional Equation
A Quick and Easy Functional Equation
Solving a Suggested Functional Equation
a functional equation /functional equation
Solving a Functional Equation
How to Simplify Rational Expressions #maths #mathematics #algebratips #gcse
Have You Solved a Functional Equation Before?
Solving Rational Equations - Step by Step Guide
How To Solve Rational Equations In Easy Steps! Gen Math and Grade 8
Solving a Functional Equation | f(x)+f(x-1)=x^2
Solving a Quick and Easy Functional Equation
A Quick and Easy Functional Equation
Math tutorial for solving rational equations
Destroying A Functional Equation Via Substitution
Rational Functions, Equations and Inequalities - Number Sense 101
How to Solve Rational Equations? General Mathematics
5 simple unsolvable equations
Solving A Functional Equation
Functional Equation
How To Solve A Functional Equation | The Easy Way
Solving Rational Equations
Комментарии
 0:06:53
0:06:53
 0:11:03
0:11:03
 0:08:51
0:08:51
 0:05:07
0:05:07
 0:06:49
0:06:49
 0:09:00
0:09:00
 0:04:42
0:04:42
 0:10:36
0:10:36
 0:00:48
0:00:48
 0:00:40
0:00:40
 0:12:20
0:12:20
 0:12:06
0:12:06
 0:08:59
0:08:59
 0:05:47
0:05:47
 0:00:45
0:00:45
 0:06:32
0:06:32
 0:00:42
0:00:42
 0:07:03
0:07:03
 0:11:35
0:11:35
 0:00:50
0:00:50
 0:00:29
0:00:29
 0:14:15
0:14:15
 0:07:19
0:07:19
 0:12:57
0:12:57