filmov
tv
f(x+y) = f(x)f(y)
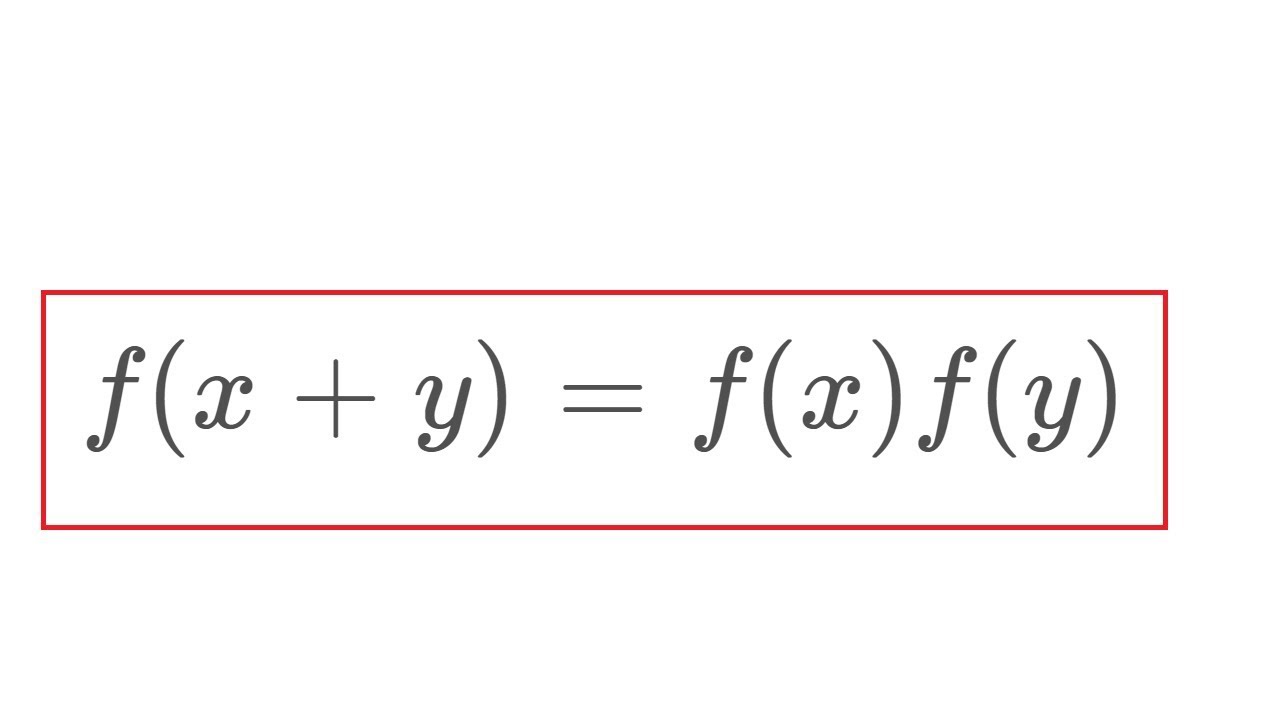
Показать описание
In this *improvised* video, I show that if is a function such that f(x+y) = f(x)f(y) and f'(0) exists, then f must either be e^(cx) or the zero function. It's amazing how we can derive all that just from such small assumptions!
This is a must-see for calculus and analysis and algebra aficionados! Enjoy!
This is a must-see for calculus and analysis and algebra aficionados! Enjoy!
Solving the Functional Equation f(x+y)=f(x)f(y)
f(x+y) = f(x)f(y)
fx+y = fx + fy
Solving the Functional Equation f(x - y) = f(x) - f(y)
Solving f(x/y)=f(x)/f(y), A Nice Functional Equation
A Functional Equation f(x+y)=f(x)+f(y)-xy
Solving the Functional Equation f(x-y)=f(x)f(y)
Solving the Functional Equation f(xy+1)=xf(y)-f(x)+6
Integrate f(x,y)=x/y over the region R bounded by x=1, x=2, y=1 and y=x² || #American #Calculus 2
Evaluate a Function from a Graph
Brain Recovery | Easy To Follow | Solving f(xy)=f(x)+f(y)
Fonksiyonlarda f(x+y)=f(x)+f(y) sağlanıyorsa ...
Exercice corrigé : équation f(x+y) = f(x) + f(y)
Solving the Functional Equation f(x+y)=xf(y)
Lost love || Demon!Yoriichi x F!Y/N || READ DEACRIPTION!
Fonksiyonlarda f(x+y)=f(x).f(y) sağlanıyorsa...
Customer Complaints (Modern AU) || Sanemi x F!Y/N || READER DESCRIPTION!!
Exercice corrigé : équation f(x+y) = f(x) + f(y) REVISITÉE
A-Level Maths: B7-17 Graphs: EDEXCEL Sketching y=f(|x|)
2nd husband 📸🔥[Archon F!Y/N x CHILDE]📸🔥[W: Flash]
Solving Cauchy's Functional Equation When f is Differentiable
A Nice Functional Equation [f(x+y)=f(x)+f(y)+2xy]
Lies || Muzan x Hindu!F!Y/N (Remake & AU) || READ DESCRIPTION!!
A Functional Equation | f(xy)=xf(y)+yf(x)
Комментарии
 0:10:18
0:10:18
 0:07:14
0:07:14
 0:17:24
0:17:24
 0:06:21
0:06:21
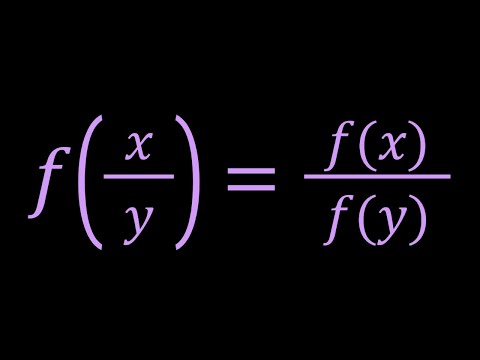 0:07:10
0:07:10
 0:07:54
0:07:54
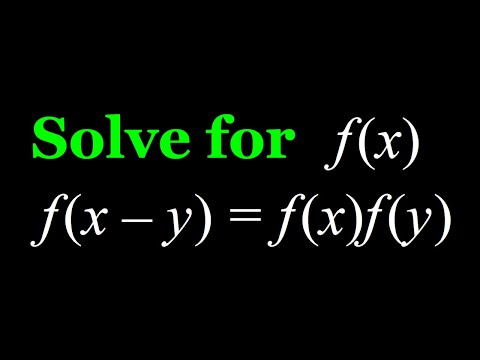 0:05:41
0:05:41
 0:05:51
0:05:51
 0:11:16
0:11:16
 0:04:29
0:04:29
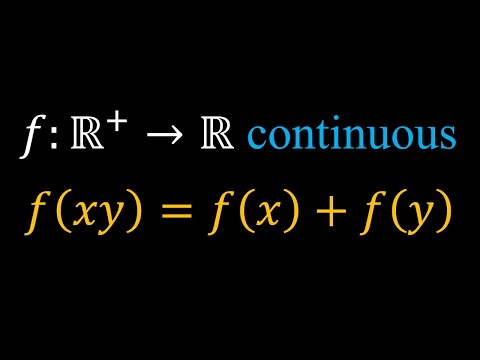 0:02:21
0:02:21
 0:03:38
0:03:38
 0:07:30
0:07:30
 0:06:11
0:06:11
 0:00:25
0:00:25
 0:02:13
0:02:13
 0:00:18
0:00:18
 0:06:11
0:06:11
 0:04:37
0:04:37
 0:00:17
0:00:17
 0:11:56
0:11:56
 0:12:10
0:12:10
 0:00:15
0:00:15
 0:08:58
0:08:58