filmov
tv
Solving f(x)+f(y)=f[(x+y)/(1-xy)]

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FunctionalEquations
PLAYLISTS 🎵 :
#ChallengingMathProblems #FunctionalEquations
PLAYLISTS 🎵 :
Solving f(x)+f(y)=f[(x+y)/(1-xy)]
Solving f(x-f(y))=1-x-y
Solving the Functional Equation f(f(x)+y)=x/(1+xy)
No Need To Lose Brain Cells| Easiest Method | f(xy)=yf(x)+xf(y)
Solving the Functional Equation f(x-y)=f(x)f(y)
Solving the Functional Equation f(xy+1)=xf(y)-f(x)+6
A Functional Equation f(x+y)=f(x)+f(y)-xy
Solving f(xy)=xf(y) in Two Ways
Relations And Functions | Class 11 Maths | NCERT Solutions
Solving The Functional Equation f(x-y) = f(x) - f(y)
Solving the functional equation f[x+f(y)]=x+y+1
if f(x)=log(1+x/1-x) then show that f(x)+f(y)=f(x + y/1+xy)
Solving an equation for y and x
A Functional Equation | f(xy)=xf(y)+yf(x)
How to Graph the Equation y = 1/x (y equals one over x)
If `f(x) + f(y) = f((x+y)/(1-xy))` for all `x, y in R (xy ne 1) and lim_(x rarr 0) (f(x))/(x) ==
First Order Partial Derivatives of f(x, y) = e^(x + y)
If `f(x)=log((1-x)/(1+x)),` show that, `f(x)+f(y)=f((x+y)/(1-x y))`
Find the Set of All Points at Which The Function is Continuous F(x, y) = sin(xy)/(e^x - y^2)
Learn Functions – Understand In 7 Minutes
5 simple unsolvable equations
Brain Recovery | Easy To Follow | Solving f(xy)=f(x)+f(y)
Total Differential of Multivariate Function f(x, y) = x^3y^4 + x^2y^3 + 12
Prove that if f(x) = log(x/(x - 1)) then f(y + 1) + f(y) = log((y + 1)/(y - 1))
Комментарии
![Solving f(x)+f(y)=f[(x+y)/(1-xy)]](https://i.ytimg.com/vi/Xyl1M40zmbs/hqdefault.jpg) 0:14:09
0:14:09
 0:06:56
0:06:56
 0:05:51
0:05:51
 0:02:57
0:02:57
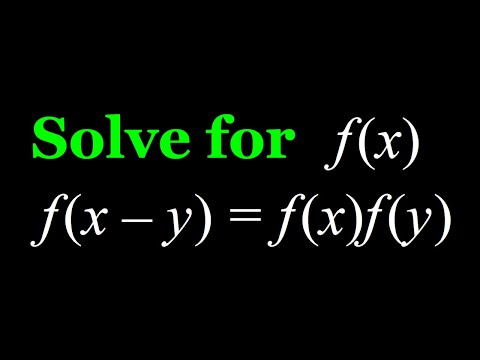 0:05:41
0:05:41
 0:05:51
0:05:51
 0:07:54
0:07:54
 0:03:27
0:03:27
 1:08:37
1:08:37
 0:03:02
0:03:02
 0:06:01
0:06:01
 0:07:48
0:07:48
 0:03:47
0:03:47
 0:08:58
0:08:58
 0:02:23
0:02:23
 0:08:54
0:08:54
 0:01:48
0:01:48
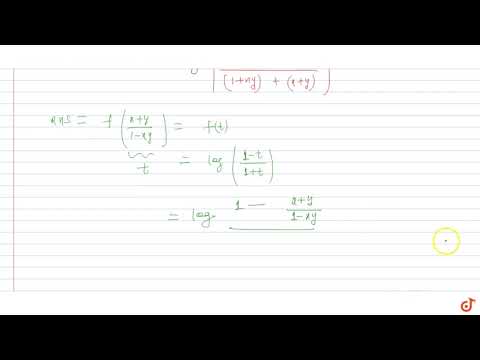 0:06:24
0:06:24
 0:02:12
0:02:12
 0:09:43
0:09:43
 0:00:50
0:00:50
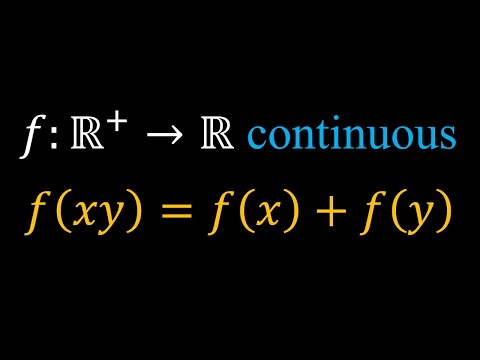 0:02:21
0:02:21
 0:01:59
0:01:59
 0:03:01
0:03:01