filmov
tv
No Need To Lose Brain Cells| Easiest Method | f(xy)=yf(x)+xf(y)
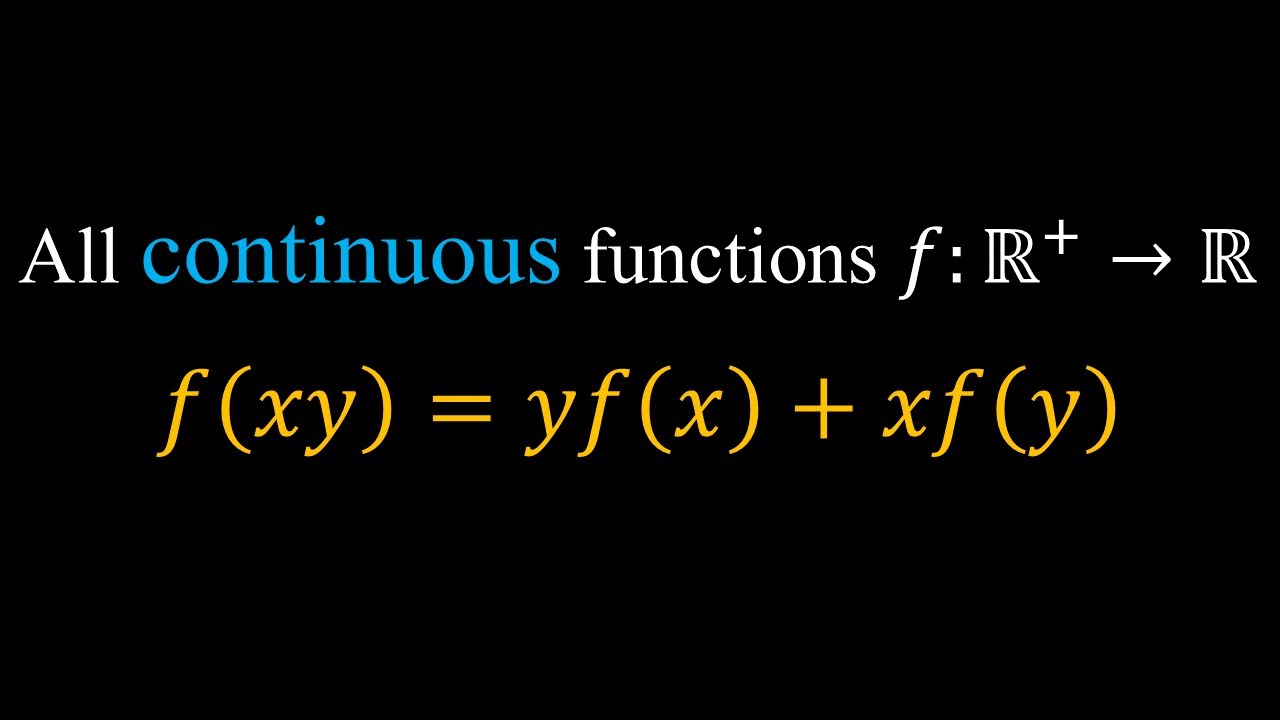
Показать описание
Hope you enjoy this video :)
I will make at least 5 videos about Functional Equation in this month. This is the 4th.
Playlist:
How To Cure 'Brain Fog' | 3 Tips for Mental Clarity
You can grow new brain cells. Here's how | Sandrine Thuret | TED
Why Your Brain Fog Never Goes Away (and How To Get Clarity)
How to protect your brain from stress | Niki Korteweg | TEDxAmsterdamWomen
Quick Way to Know if You Have Brain Damage
The Boy With No Brain | Extraordinary People | Channel 5
Could your brain repair itself? - Ralitsa Petrova
12 Signs Your Brain Is NOT Healthy
Weaponizing Emotions: The Shocking Future of Mind Control Technology!
What Losing Weight Does To Your Body And Brain | The Human Body
Reboot Your Brain in 30 Seconds
What Happens To Your Body And Brain If You Don't Get Sleep | The Human Body
What Social Isolation Does To Your Brain – How To Undo The Damage
How Can You Survive Without Part Of Your Brain?
Rihanna - Love On The Brain (Lyrics)
'Miracle Baby' Born Without Most of His Brain Defying Odds | ABC News
Recovery from Brain Injury Occurs for the Rest of a Person's Life
Brain Fog and Anxiety (how to get your mental clarity back)
5X Your BRAIN CELLS
The Main Reason Why You Get Brain Fog & Feel Confused - Dr Mandell
How stress affects your brain - Madhumita Murgia
What boxing may do to the brain
Clench Right Hand Than Left...Your Brain Will Never Forget (Memory Power) Dr. Mandell
Why does everyone want to poke the brain like that?!
Комментарии
 0:10:40
0:10:40
 0:11:05
0:11:05
 0:30:36
0:30:36
 0:09:25
0:09:25
 0:04:26
0:04:26
 0:00:21
0:00:21
 0:04:00
0:04:00
 0:14:20
0:14:20
 0:11:38
0:11:38
 0:02:24
0:02:24
 0:00:24
0:00:24
 0:04:50
0:04:50
 0:06:05
0:06:05
 0:03:56
0:03:56
 0:03:45
0:03:45
 0:07:35
0:07:35
 0:04:10
0:04:10
 0:08:29
0:08:29
 0:14:10
0:14:10
 0:05:03
0:05:03
 0:04:16
0:04:16
 0:01:36
0:01:36
 0:02:05
0:02:05
 0:00:19
0:00:19