filmov
tv
Solving f(x/y)=f(x)/f(y), A Nice Functional Equation

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FunctionalEquations
PLAYLISTS 🎵 :
#ChallengingMathProblems #FunctionalEquations
PLAYLISTS 🎵 :
Solving f(x/y)=f(x)/f(y), A Nice Functional Equation
A Nice Functional Equation [f(x+y)=f(x)+f(y)+2xy]
Solving the Functional Equation f(x+y)=f(x)f(y)
Solving f(xy)=xf(y) in Two Ways
Solving the Functional Equation f(xy+1)=xf(y)-f(x)+6
Solving the Functional Equation f(x - y) = f(x) - f(y)
A Functional Equation f(x+y)=f(x)+f(y)-xy
Solving the Functional Equation f(x-y)=f(x)f(y)
Let f:N→Y be a function defined as f(x)=4x+3, where Y={y ∈ N:y=4x+3 for some x∈ N.Find the inverse...
Range of Multivariable Function f(x, y) = x^2 + y^2
Absolute Maximum and Minimum Values of Multivariable Functions - Calculus 3
f(x+y) = f(x)f(y)
Show that the function u = f(y - kx) is a solution to the partial differential equation
Solving f(x)+f(y)=f[(x+y)/(1-xy)]
Problem Functions: y=f(x) | Lean Six Sigma Complete Course.
Solving f(x+y)=f(x)+f(y)+2xy in Two Ways
Solving the Functional Equation f(f(x)+y)=x/(1+xy)
First Order Partial Derivatives of z = f(x/y)
Solving f(sqrt(x^2+y^2))=f(x)f(y)
Lagrange Multipliers Maximize f(x,y) = 2x + 2xy + y subject to 2x + y = 100
What is a function? | Functions and their graphs | Algebra II | Khan Academy
Solving the functional equation f[x+f(y)]=x+y+1
Determine whether an equation determines y as a functions of x
Transforming Algebraic Functions: Shifting, Stretching, and Reflecting
Комментарии
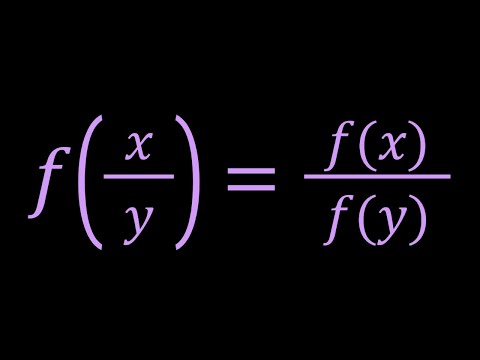 0:07:10
0:07:10
 0:12:10
0:12:10
 0:10:18
0:10:18
 0:03:27
0:03:27
 0:05:51
0:05:51
 0:06:21
0:06:21
 0:07:54
0:07:54
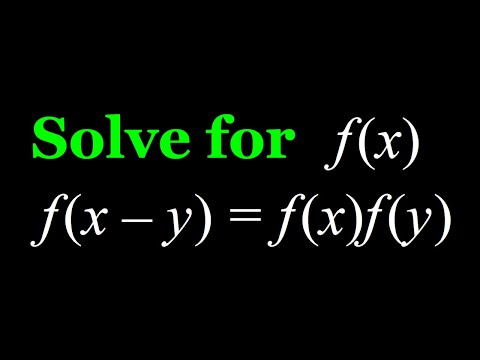 0:05:41
0:05:41
 0:02:20
0:02:20
 0:00:36
0:00:36
 0:11:24
0:11:24
 0:07:14
0:07:14
 0:03:43
0:03:43
![Solving f(x)+f(y)=f[(x+y)/(1-xy)]](https://i.ytimg.com/vi/Xyl1M40zmbs/hqdefault.jpg) 0:14:09
0:14:09
 0:03:59
0:03:59
 0:09:14
0:09:14
 0:05:51
0:05:51
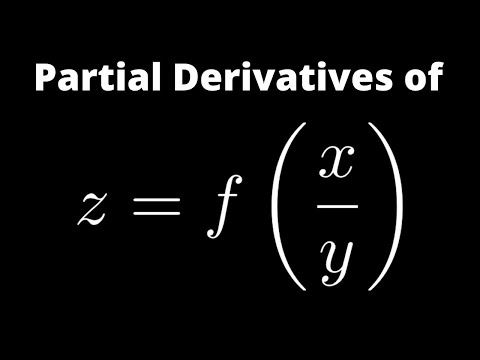 0:02:19
0:02:19
 0:08:06
0:08:06
 0:05:43
0:05:43
 0:07:57
0:07:57
 0:06:01
0:06:01
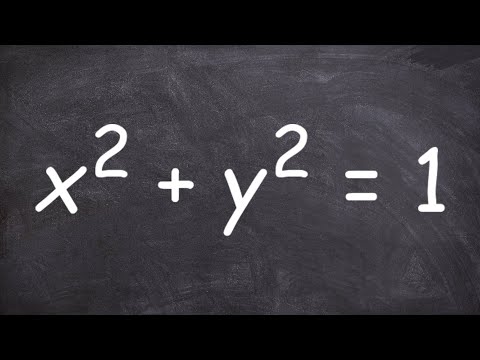 0:02:53
0:02:53
 0:07:52
0:07:52