filmov
tv
Solving the functional equation f[x+f(y)]=x+y+1

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FunctionalEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
#ChallengingMathProblems #FunctionalEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
Solving the functional equation f[x+f(y)]=x+y+1
Solving the Functional Equation f(x+y)=f(x)f(y)
Solving the Functional Equation f(xy+1)=xf(y)-f(x)+6
Solving the Functional Equation f(f(x)+y)=x/(1+xy)
Solving the Functional Equation f(x - y) = f(x) - f(y)
Solving f(x)+f(y)=f[(x+y)/(1-xy)]
Solving the Functional Equation f(x-y)=f(x)f(y)
Solving a Functional Equation | f(x)+f(x-1)=x^2
A simple yet difficult functional equation | 2020 USEMO Problem 4
A Functional Equation f(x+y)=f(x)+f(y)-xy
A Quick and Easy Functional Equation
Evaluating f(xy)=f(x)+f(y)-1
A Nice and Easy Functional Equation
Solving a Functional Equation
Solving the Functional Equation f(x+y)=xf(y)
Learn Functions – Understand In 7 Minutes
Learn about Functional Equation - Math Olympiad, ISI CMI Entrance - Concept Video - Part 1
A Functional Equation from Putnam and Beyond
A Functional Equation | f(xy)=xf(y)+yf(x)
5 simple unsolvable equations
A Curious Functional Equation | Math Olympiads
A Nice Functional Equation [f(x+y)=f(x)+f(y)+2xy]
Solving a Quick and Easy Functional Equation
A Functional Equation from British Math Olympiads 2009
Комментарии
 0:06:01
0:06:01
 0:10:18
0:10:18
 0:05:51
0:05:51
 0:05:51
0:05:51
 0:06:21
0:06:21
![Solving f(x)+f(y)=f[(x+y)/(1-xy)]](https://i.ytimg.com/vi/Xyl1M40zmbs/hqdefault.jpg) 0:14:09
0:14:09
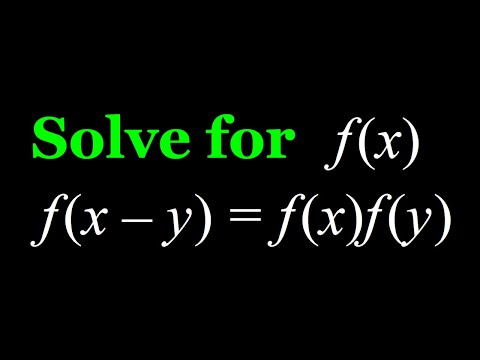 0:05:41
0:05:41
 0:08:59
0:08:59
 0:13:14
0:13:14
 0:07:54
0:07:54
 0:06:49
0:06:49
 0:04:41
0:04:41
 0:05:07
0:05:07
 0:10:36
0:10:36
 0:06:11
0:06:11
 0:09:43
0:09:43
 0:16:36
0:16:36
 0:12:07
0:12:07
 0:08:58
0:08:58
 0:00:50
0:00:50
 0:08:29
0:08:29
 0:12:10
0:12:10
 0:05:47
0:05:47
 0:08:33
0:08:33