filmov
tv
Solving f(x^y)=yf(x) | A Functional Equation
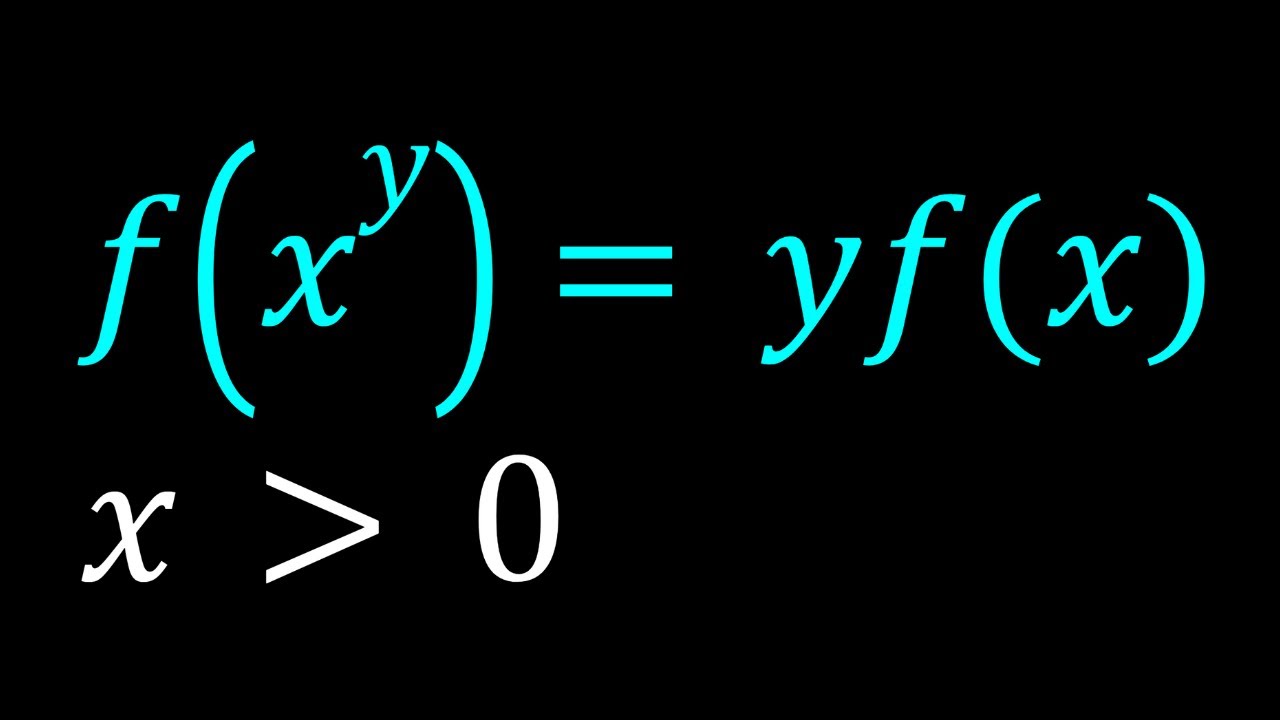
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FunctionalEquations #Functions
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
#ChallengingMathProblems #FunctionalEquations #Functions
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
Solving f(x^y)=yf(x) | A Functional Equation
No Need To Lose Brain Cells| Easiest Method | f(xy)=yf(x)+xf(y)
A Functional Equation | f(xy)=xf(y)+yf(x)
Solving f(xy)=xf(y) in Two Ways
Solving The Functional Equation f(x-y) = f(x) - f(y)
Brain Recovery | Easy To Follow | Solving f(xy)=f(x)+f(y)
Solving the Functional Equation f(x+y)=f(x)f(y)
Solving f(x/y)=f(x)/f(y), A Nice Functional Equation
Operator Method | Differential Equation | Particular Solution
Solving the Functional Equation f(x - y) = f(x) - f(y)
Solving the Functional Equation f(xy+1)=xf(y)-f(x)+6
Solving the Functional Equation f(x-y)=f(x)f(y)
Solving f(x)=yf(xy) in Two/Three Ways
Solving f(xy)=f(x)-f(1/y)
A Quick and Easy Functional Equation
Solving the Functional Equation f(f(x)+y)=x/(1+xy)
Solving the Functional Equation f(x+y)=xf(y)
solving y.f(x) = x.f(y) | solve for f(x)....!
Determine whether an equation determines y as a functions of x
Partial Derivatives of z = f(x + y)
from the PDE by eliminating f from z=e^y f(x+y)
A function f: R→ R satisfies that equation f(x + y) = f(x) f(y). Prove that f^ prime (x) = 2f(x)
A Functional Equation f(x+y)=f(x)+f(y)-xy
First Order Partial Derivatives of z = f(x/y)
Комментарии
 0:06:10
0:06:10
 0:02:57
0:02:57
 0:08:58
0:08:58
 0:03:27
0:03:27
 0:03:02
0:03:02
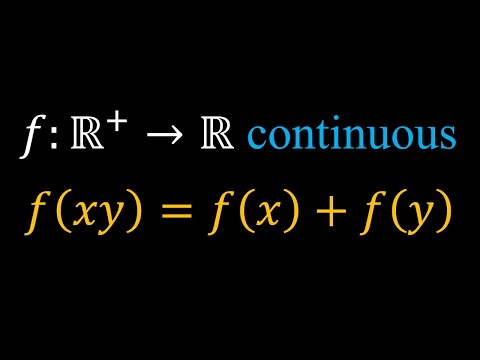 0:02:21
0:02:21
 0:10:18
0:10:18
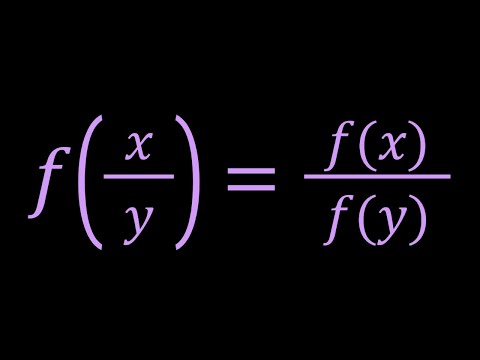 0:07:10
0:07:10
 0:17:47
0:17:47
 0:06:21
0:06:21
 0:05:51
0:05:51
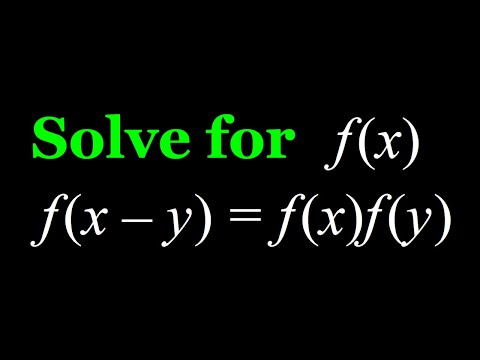 0:05:41
0:05:41
 0:08:37
0:08:37
 0:06:00
0:06:00
 0:06:49
0:06:49
 0:05:51
0:05:51
 0:06:11
0:06:11
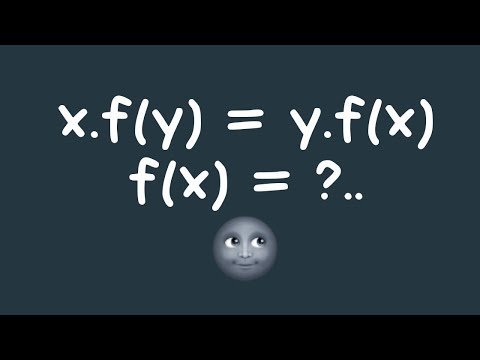 0:03:14
0:03:14
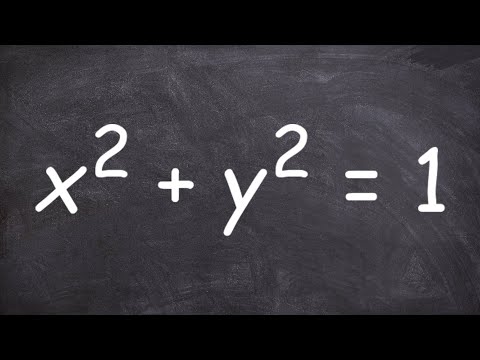 0:02:53
0:02:53
 0:01:50
0:01:50
 0:02:24
0:02:24
 0:06:29
0:06:29
 0:07:54
0:07:54
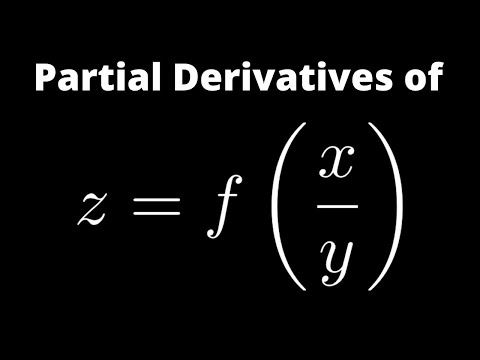 0:02:19
0:02:19