filmov
tv
A Functional Equation from British Math Olympiads 2009
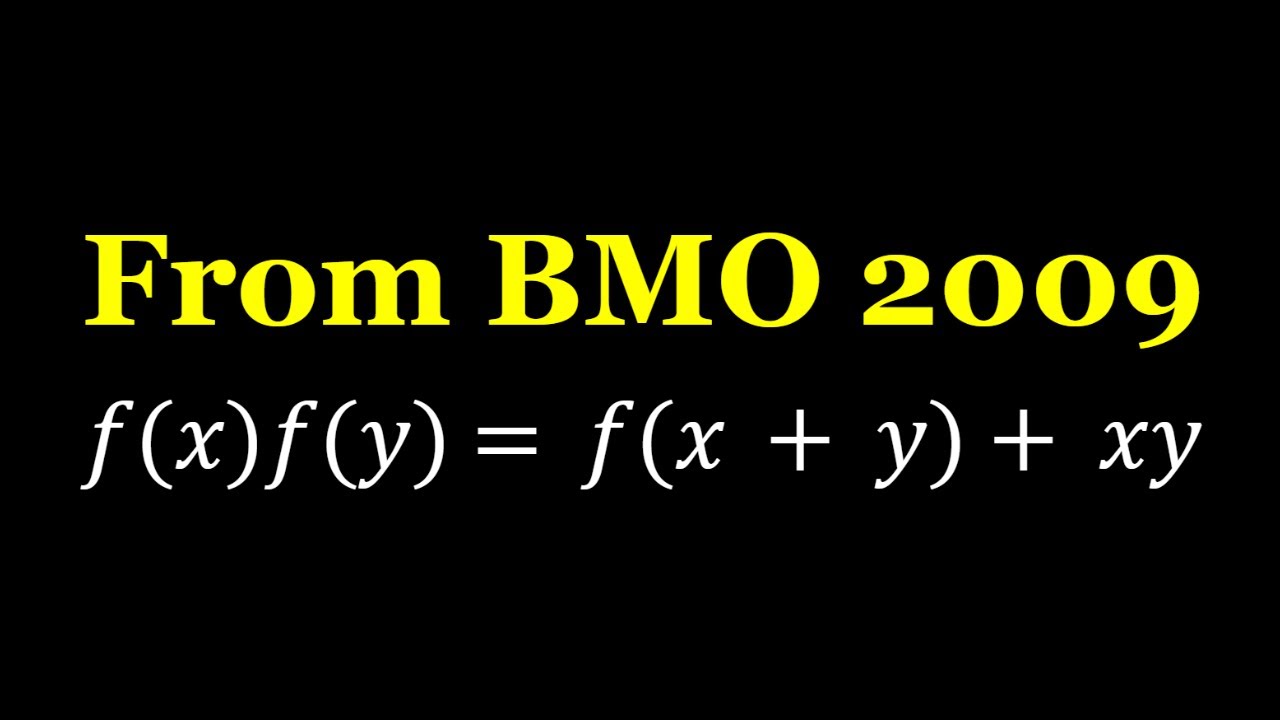
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FunctionalEquations
PLAYLISTS 🎵 :
#ChallengingMathProblems #FunctionalEquations
PLAYLISTS 🎵 :
A Functional Equation from British Math Olympiads 2009
A British Maths Olympiad Functional Equation
A nice functional equation from Romania
A functional equation from my favorite book.
Have You Solved a Functional Equation Before?
a notorious functional equation.
A Nice and Easy Functional Equation
A Quick and Easy Functional Equation
an IMO functional equation.
What is the Jensen's Functional Equation?
A Quick and Easy Functional Equation
A Functional Equation with Golden Flavor
an absolutely surprising final solution to this functional equation.
Destroying A Functional Equation Via Substitution
A fun functional equation!!
A functional equation from the Philippines.
A Functional Equation | f(x)+xf(-x)=x
a functional equation /functional equation
A Curious Functional Equation | Math Olympiads
Solving Functional Equations using Substitution Strategy | British Math Olympiad 2009 Problem 3
A Cool Functional Equation
Gaining Insights: Solving a Functional Equation
A Quick and Easy Functional Equation
Solving A Nice Functional Equation
Комментарии
 0:08:33
0:08:33
 0:09:03
0:09:03
 0:18:36
0:18:36
 0:11:23
0:11:23
 0:00:40
0:00:40
 0:19:30
0:19:30
 0:05:07
0:05:07
 0:00:45
0:00:45
 0:14:31
0:14:31
 0:00:36
0:00:36
 0:00:57
0:00:57
 0:07:21
0:07:21
 0:18:15
0:18:15
 0:00:42
0:00:42
 0:11:13
0:11:13
 0:07:44
0:07:44
 0:00:48
0:00:48
 0:04:42
0:04:42
 0:08:29
0:08:29
 0:10:08
0:10:08
 0:05:38
0:05:38
 0:10:22
0:10:22
 0:06:49
0:06:49
 0:09:50
0:09:50