filmov
tv
Solving a Functional Equation
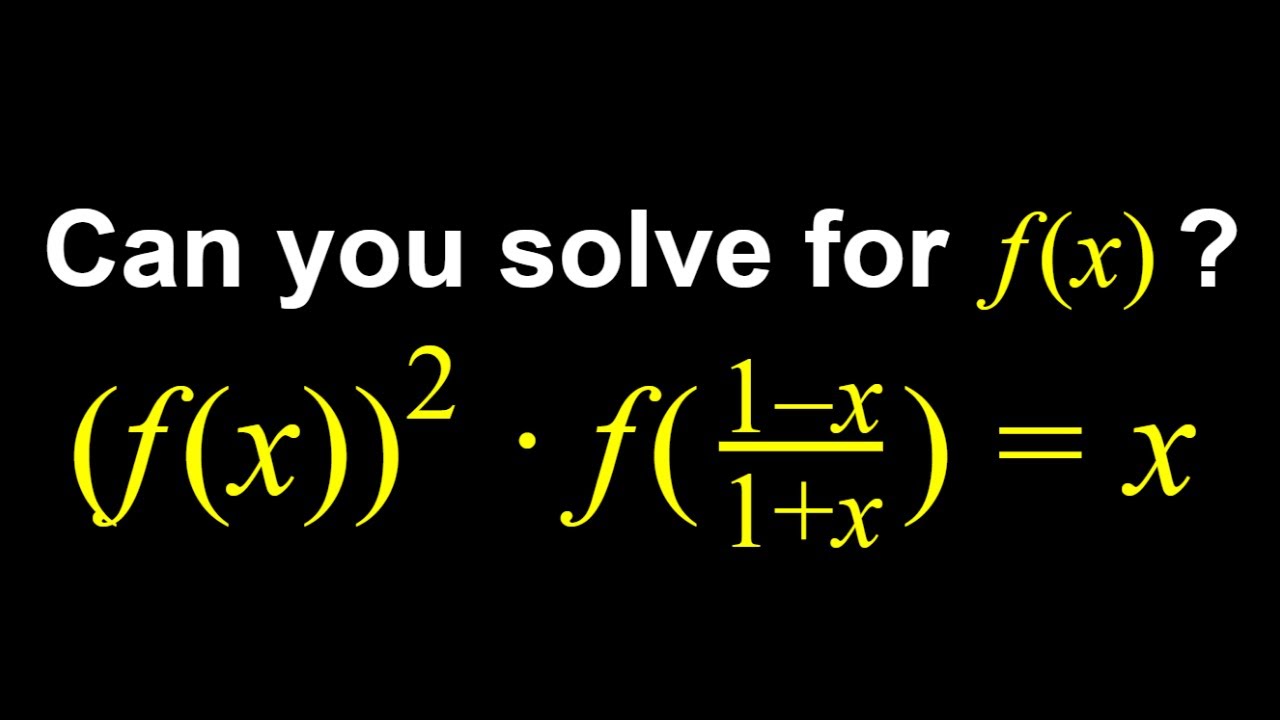
Показать описание
This video is about a Functional Equation
Send me a tweet at @SyberMath if you want to share a picture of your solution/ideas and comment here with the link to the tweet.
#ChallengingMathProblems #FunctionalEquations
EXPLORE:
Send me a tweet at @SyberMath if you want to share a picture of your solution/ideas and comment here with the link to the tweet.
#ChallengingMathProblems #FunctionalEquations
EXPLORE:
A Quick and Easy Functional Equation
Solving a Quick and Easy Functional Equation
A Nice and Easy Functional Equation
Solving a Quick and Easy Functional Equation
Solving a Functional Equation
Let's Solve A Functional Equation
the greatest functional equation of all time.
A Functional Equation from British Math Olympiads 2009
An Interesting Functional Equation | ioqm | algebra questions | how to solve maths problems quickly
Algebra Solving a Functional Equation Example
Solving the functional equation f[x+f(y)]=x+y+1
Solving a Functional Equation
Solving a Rational Functional Equation
Solving A Nice Functional Equation
Solving A Functional System of Equations in Two Ways
Solving A Functional Equation
a functional equation /functional equation
Methods of Functional Equations
Solving A Functional Equation
Lets Solve A Functional Equation
Gaining Insights: Solving a Functional Equation
Weak Spots of Functional Equations | International Mathematical Olympiad 2011 Shortlist A3
Solving a Functional Equation by Elimination
Balkan Math Olympiad 2000 - Problem 1: A classic functional equation
Комментарии
 0:06:49
0:06:49
 0:05:47
0:05:47
 0:05:07
0:05:07
 0:06:19
0:06:19
 0:10:36
0:10:36
 0:08:55
0:08:55
 0:07:48
0:07:48
 0:08:33
0:08:33
 0:13:08
0:13:08
 0:01:37
0:01:37
 0:06:01
0:06:01
 0:10:36
0:10:36
 0:06:53
0:06:53
 0:09:50
0:09:50
 0:09:27
0:09:27
 0:11:58
0:11:58
 0:04:42
0:04:42
 0:07:40
0:07:40
 0:05:56
0:05:56
 0:08:36
0:08:36
 0:10:22
0:10:22
 0:12:27
0:12:27
 0:09:08
0:09:08
 0:13:58
0:13:58