filmov
tv
Solving a Nice Functional Equation

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FunctionalEquations
PLAYLISTS 🎵 :
#ChallengingMathProblems #FunctionalEquations
PLAYLISTS 🎵 :
Solving A Nice Functional Equation
Solving A Nice Functional Equation
A Nice and Easy Functional Equation
Solving a Nice Functional Equation
Solving a Nice Functional Equation
A Quick and Easy Functional Equation
what a nice functional equation!
a nice functional equation
#How to solve exponential function#mathematics #quiz #maths
A Nice Functional Equation
A Nice And Easy Functional Equation
A Nice and Easy Functional Equation
A Functional Equation from Samara Math Olympiads
Solving For A Nice Function
A nice functional equation from Romania
Solving f(x/y)=f(x)/f(y), A Nice Functional Equation
a nice functional equation.
A Nice Functional Equation from India | Math Olympiads
Solving a Quick and Easy Functional Equation
A fun functional equation!!
A Nice Homemade Functional Equation
the greatest functional equation of all time.
A Curious Functional Equation | Math Olympiads
a fun functional equation
Комментарии
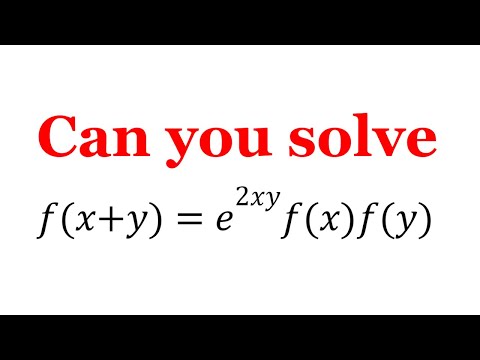 0:08:26
0:08:26
 0:09:50
0:09:50
 0:05:07
0:05:07
 0:06:28
0:06:28
 0:06:58
0:06:58
 0:06:49
0:06:49
 0:10:10
0:10:10
 0:11:25
0:11:25
 0:01:01
0:01:01
 0:08:45
0:08:45
 0:10:51
0:10:51
 0:08:14
0:08:14
 0:08:47
0:08:47
 0:08:39
0:08:39
 0:18:36
0:18:36
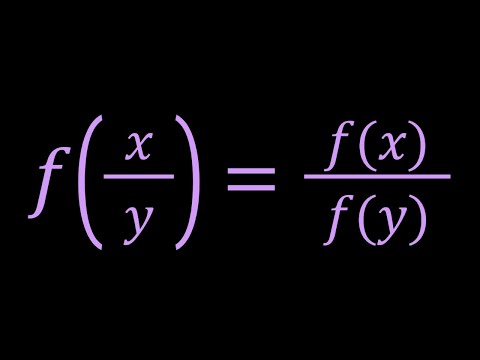 0:07:10
0:07:10
 0:18:42
0:18:42
 0:09:24
0:09:24
 0:05:47
0:05:47
 0:11:13
0:11:13
 0:09:22
0:09:22
 0:07:48
0:07:48
 0:08:29
0:08:29
 0:09:20
0:09:20