filmov
tv
A Nice Functional Equation from India | Math Olympiads
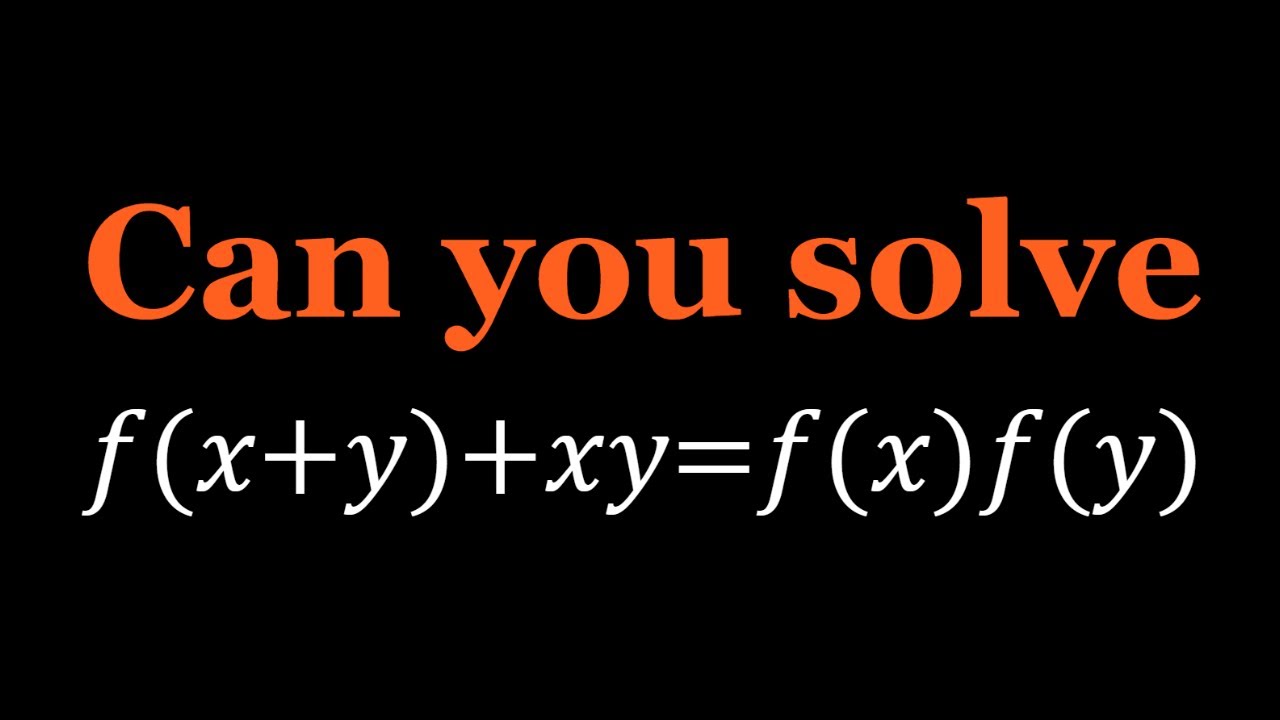
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FunctionalEquations #Functions
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FunctionalEquations #Functions
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
a nice functional equation
A nice functional equation from Romania
Solving A Nice Functional Equation
A Nice and Easy Functional Equation
the greatest functional equation of all time.
A functional equation from my favorite book.
a nice functional equation.
a fun functional equation
A Nice Algebra Exponential problem || maths olympiad questions || find value of x
A Nice Functional Equation
A Functional Equation from Samara Math Olympiads
what a nice functional equation!
Solving A Nice Functional Equation
A Functional Equation from Türkiye 🇹🇷
One of the coolest functional equations I have seen!
Solving a Nice Functional Equation
A fun functional equation!!
A functional equation from @goodplacetostop2973
A nice functional equation from the Balkan math olympiad
A Nice Functional Equation from India | Math Olympiads
a notorious functional equation.
A functional equation from the Philippines.
Another Nice Functional Equation #algebra
A Nice and Easy Functional Equation
Комментарии
 0:11:25
0:11:25
 0:18:36
0:18:36
 0:09:50
0:09:50
 0:05:07
0:05:07
 0:07:48
0:07:48
 0:11:23
0:11:23
 0:18:42
0:18:42
 0:09:20
0:09:20
 0:04:12
0:04:12
 0:08:45
0:08:45
 0:08:47
0:08:47
 0:10:10
0:10:10
 0:08:26
0:08:26
 0:08:55
0:08:55
 0:15:34
0:15:34
 0:06:28
0:06:28
 0:11:13
0:11:13
 0:08:18
0:08:18
 0:05:29
0:05:29
 0:09:24
0:09:24
 0:19:30
0:19:30
 0:07:44
0:07:44
 0:05:51
0:05:51
 0:08:14
0:08:14