filmov
tv
A Functional Equation from Samara Math Olympiads
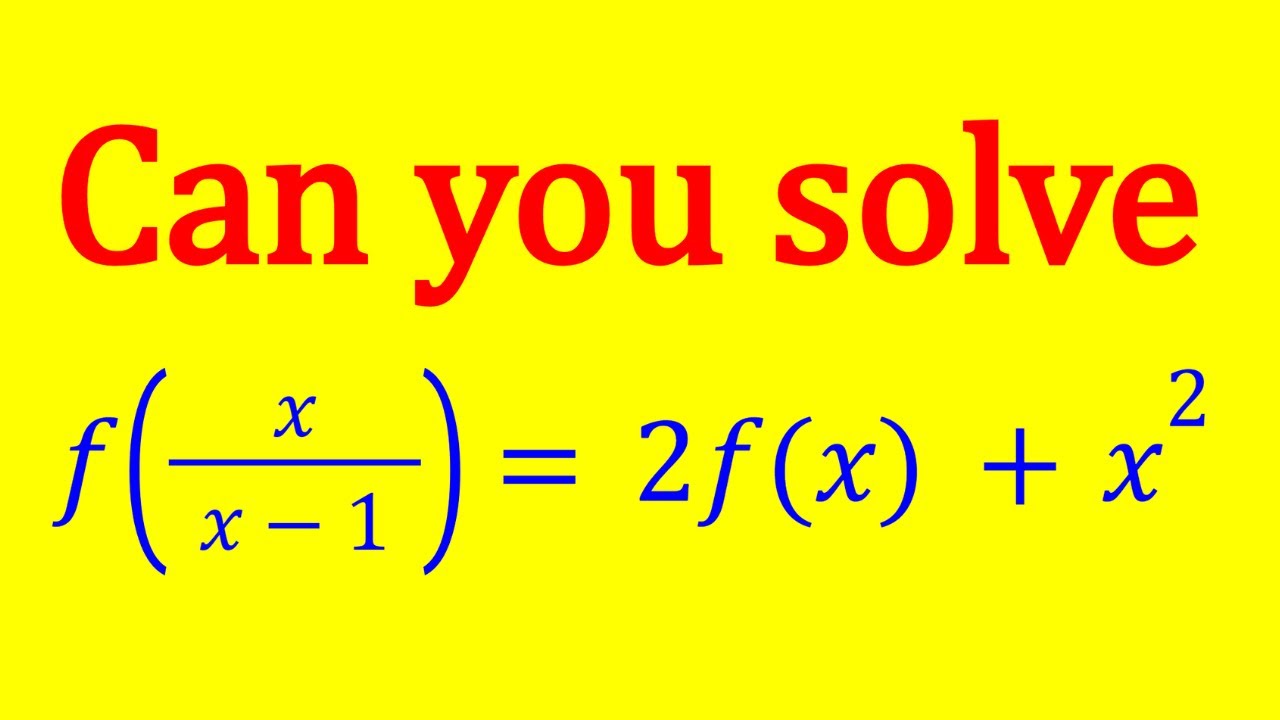
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (aplusbi)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
When you purchase something from here, I will make a small percentage of commission that helps me continue making videos for you.
If you are preparing for Math Competitions and Math Olympiads, then this is the page for you!
CHECK IT OUT!!! ❤️ ❤️ ❤️
❤️ f(x/(x-1)) = 2f(x) + x^2
If you need to post a picture of your solution or idea:
#radicals #radicalequations #algebra #calculus #differentialequations #polynomials #prealgebra #polynomialequations #numbertheory #diophantineequations #comparingnumbers #trigonometry #trigonometricequations #complexnumbers #math #mathcompetition #olympiad #matholympiad #mathematics #sybermath #aplusbi #shortsofsyber #iit #iitjee #iitjeepreparation #iitjeemaths #exponentialequations #exponents #exponential #exponent #systemsofequations #systems
#functionalequations #functions #function #maths #counting #sequencesandseries
#algebra #numbertheory #geometry #calculus #counting #mathcontests #mathcompetitions
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
When you purchase something from here, I will make a small percentage of commission that helps me continue making videos for you.
If you are preparing for Math Competitions and Math Olympiads, then this is the page for you!
CHECK IT OUT!!! ❤️ ❤️ ❤️
❤️ f(x/(x-1)) = 2f(x) + x^2
If you need to post a picture of your solution or idea:
#radicals #radicalequations #algebra #calculus #differentialequations #polynomials #prealgebra #polynomialequations #numbertheory #diophantineequations #comparingnumbers #trigonometry #trigonometricequations #complexnumbers #math #mathcompetition #olympiad #matholympiad #mathematics #sybermath #aplusbi #shortsofsyber #iit #iitjee #iitjeepreparation #iitjeemaths #exponentialequations #exponents #exponential #exponent #systemsofequations #systems
#functionalequations #functions #function #maths #counting #sequencesandseries
#algebra #numbertheory #geometry #calculus #counting #mathcontests #mathcompetitions
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Комментарии
 0:08:47
0:08:47
 0:03:09
0:03:09
 0:08:06
0:08:06
 0:00:40
0:00:40
 0:01:56
0:01:56
 0:07:06
0:07:06
 0:05:39
0:05:39
 0:36:00
0:36:00
 0:10:06
0:10:06
 0:05:26
0:05:26
 0:03:48
0:03:48
 0:04:37
0:04:37
 0:12:04
0:12:04
 0:06:03
0:06:03
 0:30:09
0:30:09
 0:06:42
0:06:42
 0:16:52
0:16:52
 0:06:12
0:06:12
 0:04:56
0:04:56
 0:18:09
0:18:09
 0:04:37
0:04:37
 0:24:17
0:24:17
 0:11:04
0:11:04
 1:07:14
1:07:14