filmov
tv
a fun functional equation

Показать описание
🌟Support the channel🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
A fun functional equation!!
a fun functional equation
Solving A Fun Functional Equation
A Fun Functional Equation
the greatest functional equation of all time.
Solving A Quick and Fun Functional Equation
a fun functional equation with an inverse twist
A Cool Functional Equation
#differentiation #class12 #maths #shorts
A Nice and Easy Functional Equation
A functional equation from my favorite book.
Fun Functional Equation to Solve with Easy Algebraic Skills
A super interesting functional equation
A Curious Functional Equation | Math Olympiads
An interesting Functional equation
Solving a Quick and Easy Functional Equation
A Quick and Easy Functional Equation
A Functional Equation from British Math Olympiads 2009
Solving a Suggested Functional Equation
Solving an Interesting Functional Equation
How REAL Men Integrate Functions
A Homemade Functional Equation from @SyberMath 😁
Visualization of the solutions to the functional equation
CMU Putnam Seminar 10/2 Functional Equations
Комментарии
 0:11:13
0:11:13
 0:09:20
0:09:20
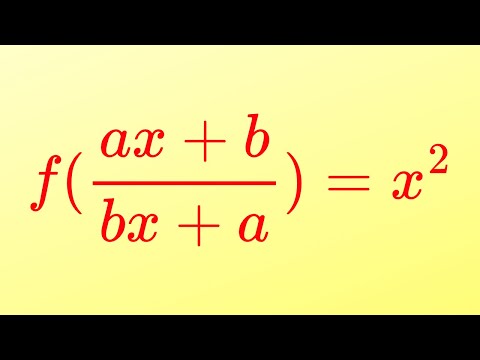 0:09:14
0:09:14
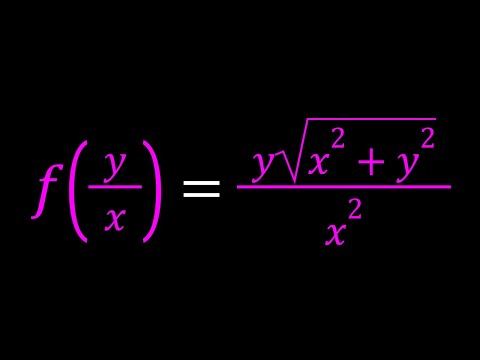 0:10:19
0:10:19
 0:07:48
0:07:48
 0:03:56
0:03:56
 0:16:41
0:16:41
 0:12:43
0:12:43
 0:00:56
0:00:56
 0:05:07
0:05:07
 0:11:23
0:11:23
 0:06:20
0:06:20
 0:03:27
0:03:27
 0:08:29
0:08:29
 0:10:58
0:10:58
 0:05:47
0:05:47
 0:06:49
0:06:49
 0:08:33
0:08:33
 0:09:00
0:09:00
 0:09:49
0:09:49
 0:00:35
0:00:35
 0:09:48
0:09:48
 0:11:35
0:11:35
 0:58:00
0:58:00