filmov
tv
A Nice Equation with Integer Solutions

Показать описание
If you need to post a picture of your solution or idea:
#NumberTheoryProblems #DiophantineEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
#NumberTheoryProblems #DiophantineEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
A Nice Equation with Integer Solutions
A Nice Equation with Integer Solutions
A Nice Diophantine Equation in Number Theory | You Should Learn This Theorem | Math Olympiad
The Most Wholesome Math Equation
An Equation with Integer Solutions? (b^2-4ac=23)
A Rational Equation with Integer Solutions (3/x)+(5/y)=4
Diophantine Equation: ax+by=gcd(a,b) ← Number Theory
How to Solve One-Step Equations | One-Step Equation Steps | Math with Mr. J
Saying 'I Love You' in Maths Equation
An Equation with Integer Solutions
United Kingdom - A Nice Exponential Equation | Math olympiad Question
a nice integral equation.
The Most Beautiful Equation in Math
Finding an Equation with Integer Coefficients from a Root
A nice suggested differential equation
Move 1 pencil to make the equation true✏️ 🤣🤣🤣 #Trivia #FatherSon #Comedy #TBfunnyASF
A Nice Exponential Equation (e^x=x^e)
A Linear Diophantine Equation
A Nice Exponential Equation (5^x-3^x=16)
Finding Positive Integer Solutions to an Equation (x+y+z=xyz)
Example 2 Integer solutions of an equation
Solving an equation for y and x using two steps
A Nice Exponential Equation
Solving A Nice Exponential Equation
Комментарии
 0:07:34
0:07:34
 0:06:26
0:06:26
 0:07:40
0:07:40
 0:00:16
0:00:16
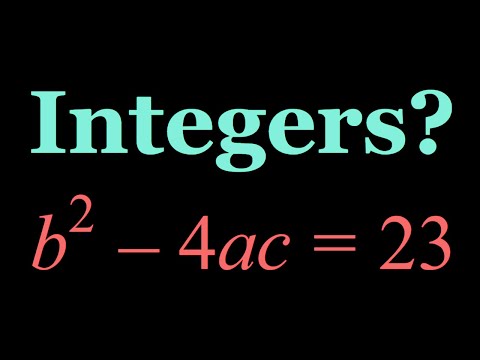 0:05:28
0:05:28
 0:08:16
0:08:16
 0:09:43
0:09:43
 0:06:54
0:06:54
 0:00:50
0:00:50
 0:10:17
0:10:17
 0:09:19
0:09:19
 0:10:44
0:10:44
 0:03:50
0:03:50
 0:08:56
0:08:56
 0:11:41
0:11:41
 0:01:01
0:01:01
 0:09:59
0:09:59
 0:10:24
0:10:24
 0:06:37
0:06:37
 0:09:19
0:09:19
 0:10:53
0:10:53
 0:03:12
0:03:12
 0:01:00
0:01:00
 0:06:30
0:06:30