filmov
tv
A Nice Exponential Equation (5^x-3^x=16)

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts) and my first video in short form! Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ExponentialEquations
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
A SIMILAR PROBLEM:
EXPLORE 😎:
PLAYLISTS 🎵 :
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ExponentialEquations
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
A SIMILAR PROBLEM:
EXPLORE 😎:
PLAYLISTS 🎵 :
A Nice Exponential Equation (5^x-3^x=16)
A Nice Exponential Equation (5^x-3^x=16)
A nice exponential equation || 5^x-3^x=16
A Nice Exponential Equation 5^x - 3^x=16 (Solved in a most unusual way)
A Nice Exponential Equation (5^x-3^x = 16) || Can you solve it?
Solve for x. Exponential Equation. 5^x - 3^x = 16.
A Nice Olympiad Math Problem 5^x - 3^x= 16 | You should know how to solve this problem
5^(x) - 3^(x) = 16 | Exponential Equation | Algebra
Math Olympiad | A Beautiful Exponential Problem | VIJAY Maths
A Nice Exponential Equation 5^x - 3^x=16 (Solved By Using Pythagorean Theorem)
A Nice Exponential Equation Maths Olympiad | 5^x-3^x=16, x=?
Équation 5^x-3^x=16
A Nice Exponential Equation (5^x-3^x=16)
Solve Fast! | 16^x +16^x=1/4; Find x | Exponential Equations | Algebra Problems
An Exponential Equation (5^x-3^x=16) | How to solve an Exponential Equation | Ali Zubair
A nice exponential math Olympiad question | You can also try this😃 | @codehorse
Tricky Exponential Problem
Can You Solve for X in 5^x=2e^x? | Exponential Equation | SAT Math Problem
Solve an exponential equation by taking log of both sides & approximating the value
Exponential Equations - Algebra and Precalculus
Solving Exponential Equation @KasyannoEZMath
A Nice Exponential Equation | Solve x^3–5=3. | Exponential Equation.
A Nice Math Olympiad Exponential Equation 3^x = X^9
solving 2^x=3^(x+1)
Комментарии
 0:06:37
0:06:37
 0:02:19
0:02:19
 0:09:50
0:09:50
 0:09:17
0:09:17
 0:08:02
0:08:02
 0:07:22
0:07:22
 0:08:57
0:08:57
 0:05:58
0:05:58
 0:07:44
0:07:44
 0:03:00
0:03:00
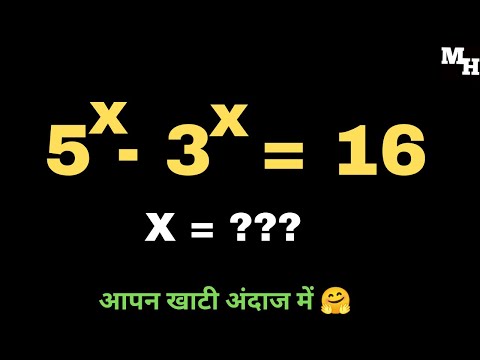 0:08:19
0:08:19
 0:01:05
0:01:05
 0:02:59
0:02:59
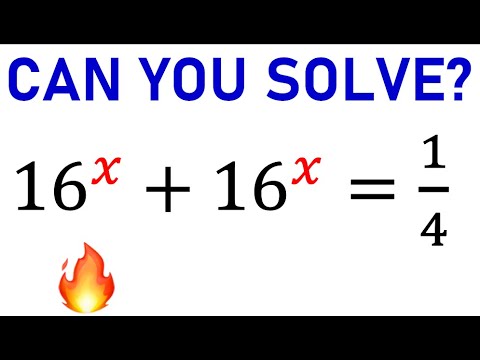 0:02:49
0:02:49
 0:06:24
0:06:24
 0:01:52
0:01:52
 0:00:55
0:00:55
 0:04:12
0:04:12
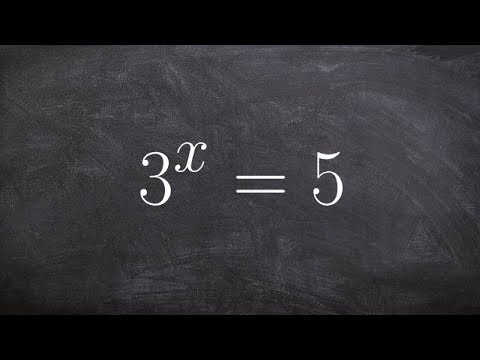 0:03:23
0:03:23
 0:05:58
0:05:58
 0:00:54
0:00:54
 0:09:36
0:09:36
 0:02:34
0:02:34
 0:00:41
0:00:41