filmov
tv
An Equation with Integer Solutions? (b^2-4ac=23)

Показать описание
If you need to post a picture of your solution or idea:
#NumberTheoryProblems #DiophantineEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
#NumberTheoryProblems #DiophantineEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
An Equation With Integer Solutions
An Equation With Integer Solutions
A Nice Equation with Integer Solutions
An Equation with Integer Solutions? (b^2-4ac=23)
How to Find Integer Solutions of this Equation?
Solving a cubic equation and looking for integer solutions. Substitution rules.
A Nice Diophantine Equation in Number Theory | You Should Learn This Theorem | Math Olympiad
A Nice Diophantine Equation | Integer Solutions
Another NICE solution using 2024
Example 2 Integer solutions of an equation
A Diophantine Equation with Integer Solutions
A Rational Equation with Integer Solutions (3/x)+(5/y)=4
Number of solutions to linear equations | Linear equations | Algebra I | Khan Academy
Can You Find Integer Solutions? | Diophantine Equations | Math Olympiad Training
Solving a Diophantine Equation by Factoring | Solve for Integer Solutions #NumberTheory
Math Olympiad | How to Find Integer Solutions to the Exponential Equation?
Example 10 Integer solutions of an equation
An Equation with Integer Solutions
A System of Equations with Integer Solutions
Find All the Integer Solutions | Use This Tricks
A Nice Equation with Integer Solutions
Diophantine Equation: ax+by=gcd(a,b) ← Number Theory
Solving a Diophantine Equation From USA | y^3-2x^2=1388 Solve For Integer Solutions | Math Olympiad
Number of Non-Negative Integer Solutions of linear Equation Part 1
Комментарии
 0:08:40
0:08:40
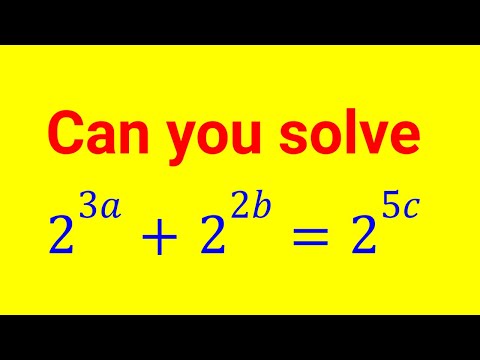 0:09:23
0:09:23
 0:07:34
0:07:34
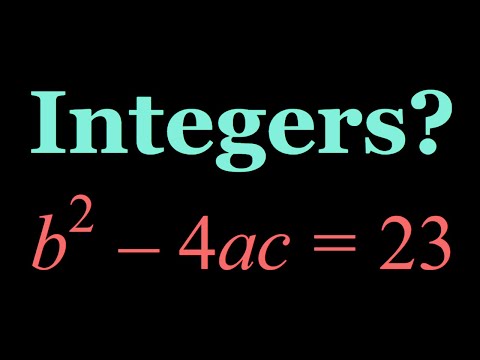 0:05:28
0:05:28
 0:02:43
0:02:43
 0:08:46
0:08:46
 0:07:40
0:07:40
 0:09:46
0:09:46
 0:07:51
0:07:51
 0:10:53
0:10:53
 0:00:49
0:00:49
 0:08:16
0:08:16
 0:05:27
0:05:27
 0:01:54
0:01:54
 0:07:08
0:07:08
 0:03:49
0:03:49
 0:08:06
0:08:06
 0:10:17
0:10:17
 0:04:40
0:04:40
 0:03:50
0:03:50
 0:06:26
0:06:26
 0:09:43
0:09:43
 0:04:40
0:04:40
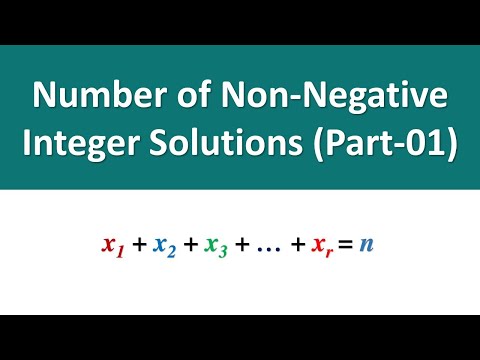 0:06:01
0:06:01