filmov
tv
Finding Positive Integer Solutions to an Equation (x+y+z=xyz)

Показать описание
If you need to post a picture of your solution or idea:
#NumberTheoryProblems #DiophantineEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
#NumberTheoryProblems #DiophantineEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
Finding Positive Integer Solutions to an Equation (x+y+z=xyz)
Solve the Rational Equation for positive integer solutions.
Number of Positive Integer Solutions How to Find Part 2
Find all Positive Integer Solutions
PotW: Finding a Positive Integer Solution [Number Theory]
Positive Integer Solutions?
A Diophantine Equation | Find Positive Integer Solutions
🔍 Positive Integer Solutions: Solving 11x + 13y = 369 Equation
Digital SAT Blue Book Practice Test 5 Math Module 2 Hard fully explained
Find positive integer solutions: 1/x + 1/y = 1/5
A Nice Math Problem|| X = ?, Y= ? || Find Positive Integer Solutions
Adding Integers | How to Add Positive and Negative Integers
Number of positive integer solutions | Combinatorics | Easy
An Equation With Integer Solutions
Number of Non-Negative Integer Solutions of linear Equation Part 1
Find all positive integer solutions to floor(x/9) = floor(x/11); Black Book, Function Problem 54
🔢 Counting Positive Integer Solutions: Solving 29x + 40y = 500 Equation
SLST Mathematics | Short Tricks | Linear Diophantine Equation. Find positive integer solutions...
Number of positive integer solutions `(x, y, z)` of `xyz=18` is
Inequality Proofs (Example 1 of 5: How many positive integer solutions?)
Number of Non-Negative Integer solutions of the equation x + y + z = 10 | General Case Explained
FIND THE NUMBER OF INTEGER SOLUTIONS OF THE EQUATION X1+X2+X3+X4+X5=30
How Many Positive Integer Solutions? | Sticks and Stones
The number of ordered triplets of positive integers which are solution of the equation x+y+z=100 is:
Комментарии
 0:09:19
0:09:19
 0:04:55
0:04:55
 0:03:27
0:03:27
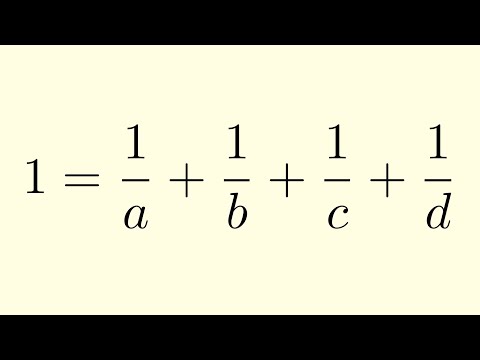 0:11:17
0:11:17
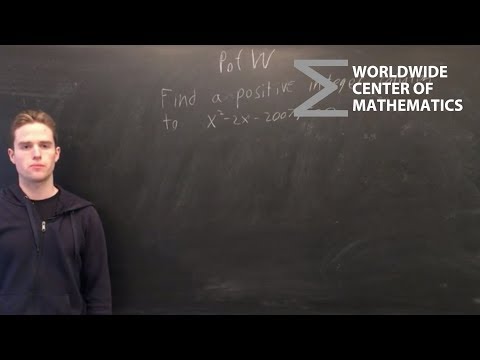 0:01:53
0:01:53
 0:02:07
0:02:07
 0:06:11
0:06:11
 0:01:29
0:01:29
 1:12:14
1:12:14
 0:05:59
0:05:59
 0:07:06
0:07:06
 0:06:46
0:06:46
 0:06:12
0:06:12
 0:08:40
0:08:40
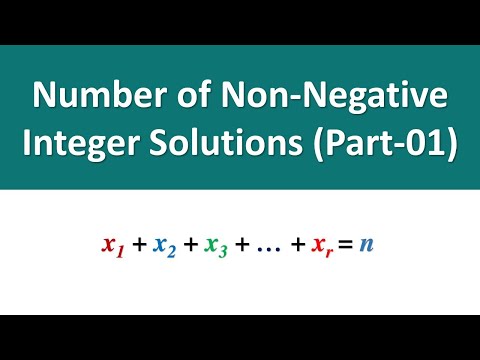 0:06:01
0:06:01
 0:05:31
0:05:31
 0:01:58
0:01:58
 0:07:42
0:07:42
 0:02:24
0:02:24
 0:11:07
0:11:07
 0:09:41
0:09:41
 0:12:40
0:12:40
 0:07:22
0:07:22
 0:03:43
0:03:43