filmov
tv
United Kingdom - A Nice Exponential Equation | Math olympiad Question
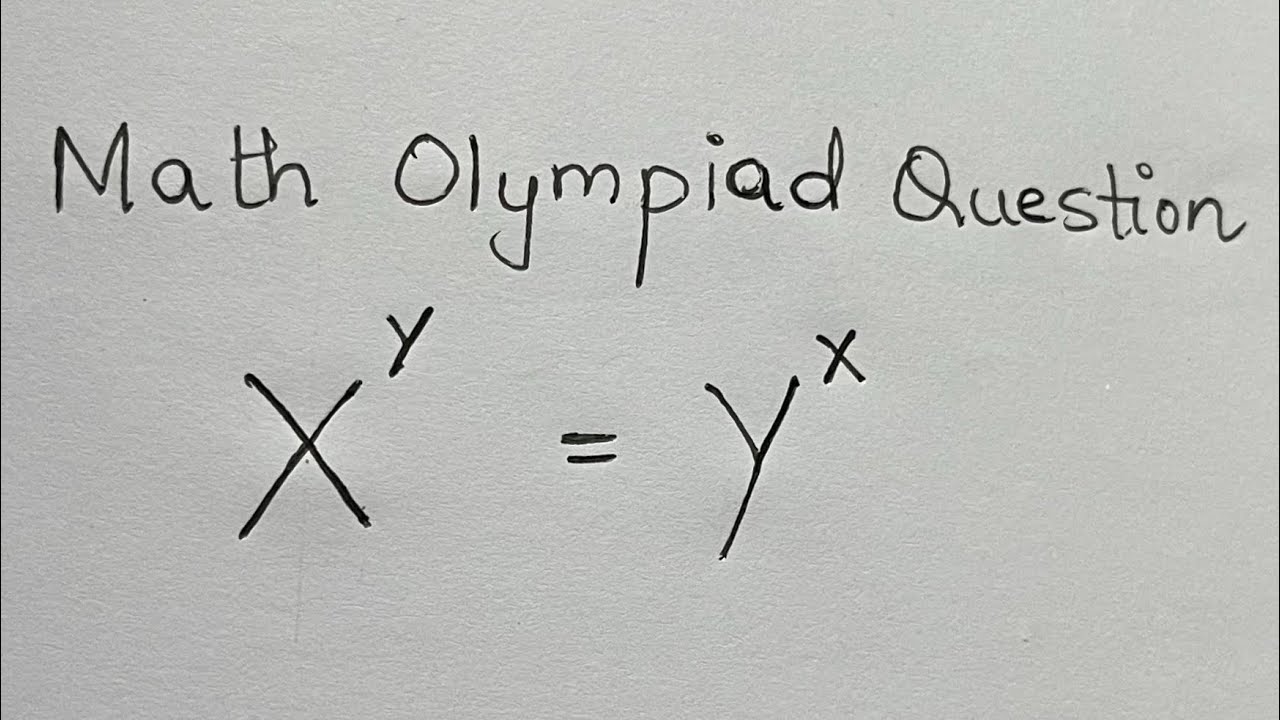
Показать описание
A Nice Exponential Equation solving
Top 27 Places To Visit In United Kingdom - UK Travel Guide
20 Interesting Facts about the United Kingdom | UK Fun Facts
Olly Alexander - Dizzy (LIVE) | United Kingdom 🇬🇧 | Grand Final | Eurovision 2024
United Kingdom - A Nice Exponential Equation | Math olympiad Question
UK | United Kingdom | United Kingdom Song | A Geography Song About the UK and its Capitals
United Kingdom: Geography, Nature, Culture & Facts || England, Scotland, Wales & Northern Ir...
UNITED KINGDOM SEASON 3 ( New Movie) Uju Okoli - 2024 Latest Nigerian Nollywood Movie
10 Best Places to Live in the United Kingdom
United Kingdom| Top 5 | Places to Visit in 2024| very beautiful places #travel #tour
Did you know in that United Kingdom....
THE UNITED KINGDOM
Difference Between United Kingdom, Great Britain and England
United Kingdom | Basic Information | Everyone Must Know
Here’s the difference between Great Britain, the United Kingdom, and England
The United Kingdom 4K - Scenic Relaxation Film With Calming Music
UK | The United Kingdom | Primary & Elementary | England | Scotland | Wales | Northern Ireland
The United Kingdom - an ESL World Adventure
One Woman, 17 British Accents - Anglophenia Ep 5
United Kingdom | Math Olympiad | A Nice Algebra Problem | Exponent Root Simplification👇👇👇
What's the difference between Great Britain and United Kingdom?
'United Kingdom Song' with signing | By Al Start | Primary School Geography
United Kingdom: Top 5 Hidden Holiday Destinations 💎🧳✈️🗺🇬🇧
Top 10 Cities to Visit in UK | United Kingdom
United Kingdom has the BEST Geography...🇬🇧🇬🇧
Комментарии
 0:30:22
0:30:22
 0:03:05
0:03:05
 0:03:28
0:03:28
 0:09:19
0:09:19
 0:01:25
0:01:25
 0:05:01
0:05:01
 0:54:20
0:54:20
 0:09:32
0:09:32
 0:02:34
0:02:34
 0:00:14
0:00:14
 0:19:25
0:19:25
 0:02:27
0:02:27
 0:02:21
0:02:21
 0:00:53
0:00:53
 1:00:49
1:00:49
 0:08:55
0:08:55
 0:02:32
0:02:32
 0:05:20
0:05:20
 0:09:00
0:09:00
 0:00:43
0:00:43
 0:04:05
0:04:05
 0:07:40
0:07:40
 0:15:23
0:15:23
 0:00:25
0:00:25