filmov
tv
A Nice Diophantine Equation in Number Theory | You Should Learn This Theorem | Math Olympiad

Показать описание
In this video, I am introducing a nice diophantine equation in number theory and also a wonderful theorem you can use to solve a linear diophantine equation with two unknown variables. With this theorem, most of the linear diophantine equations with two unknown variables will be nicely solved. Diophantine equation is an interesting topic in number theory. Come check this video out and watch it until the end. This would also be a good practice for math olympiad. More with diophantine equation problems will come! Stay tuned!
💬 Did you enjoy this video? Tell me all about it in the comment section below!
Subscribe to Dr. PK Math here ⤵️
*************
✅ Follow Modern Dr PK Math on social media:
*************
#DrPKMath #diophantineequation #matholympiad
💬 Did you enjoy this video? Tell me all about it in the comment section below!
Subscribe to Dr. PK Math here ⤵️
*************
✅ Follow Modern Dr PK Math on social media:
*************
#DrPKMath #diophantineequation #matholympiad
A Nice Diophantine Equation in Number Theory | You Should Learn This Theorem | Math Olympiad
A Nice Diophantine Equation | 1st method
A Nice Diophantine Equation
A Nice Diophantine Equation in Number Theory You Will Never Forget
A Nice Diophantine Equation
Solving a Nice Diophantine Equation in Three Ways
A Nice Diophantine Equation | Integer Solutions
what a nice Diophantine equation.
A Diophantine Equation @pkqualitymath1234
Number Theory | Linear Diophantine Equations
Diophantine Equation: ax+by=gcd(a,b) ← Number Theory
Solve Diophantine Equations by Factoring
Solving A Nice Diophantine Equation from Romania
Solving A Nice Diophantine Equation | Integer Solutions
A Nice Diophantine Equation from Russian Math Olympiad with Interesting Skills You Should Know
A Nice Diophantine Equation | 2nd method
Diophantine Equations: Strategies and Examples
A Nice Diophantine Equation | Greece Junior Mathematical Olympiad
a nice 'mixed' Diophantine equation
Solving a Nice Diophantine Equation in Number Theory
a nice exponential Diophantine equation -- #maths
A Diophantine Equation | x^2-y^2=23
A Nice Diophantine Equation | Math Olympiad Preparation | Challenging Algebraic Problem.
A Diophantine Equation | a^2=b^2+13
Комментарии
 0:07:40
0:07:40
 0:07:39
0:07:39
 0:08:56
0:08:56
 0:08:06
0:08:06
 0:08:57
0:08:57
 0:08:13
0:08:13
 0:09:46
0:09:46
 0:12:33
0:12:33
 0:14:11
0:14:11
 0:09:17
0:09:17
 0:09:43
0:09:43
 0:01:58
0:01:58
 0:09:09
0:09:09
 0:09:35
0:09:35
 0:08:26
0:08:26
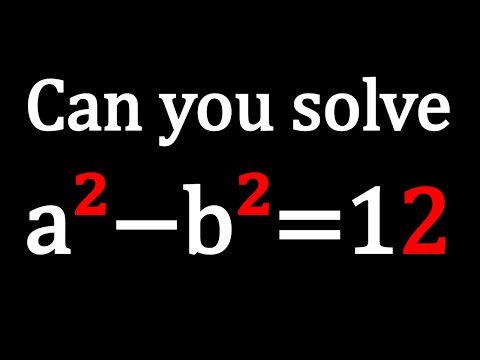 0:04:08
0:04:08
 0:27:34
0:27:34
 0:09:55
0:09:55
 0:12:20
0:12:20
 0:04:25
0:04:25
 0:00:54
0:00:54
 0:00:55
0:00:55
 0:06:37
0:06:37
 0:00:46
0:00:46