filmov
tv
A Linear Diophantine Equation
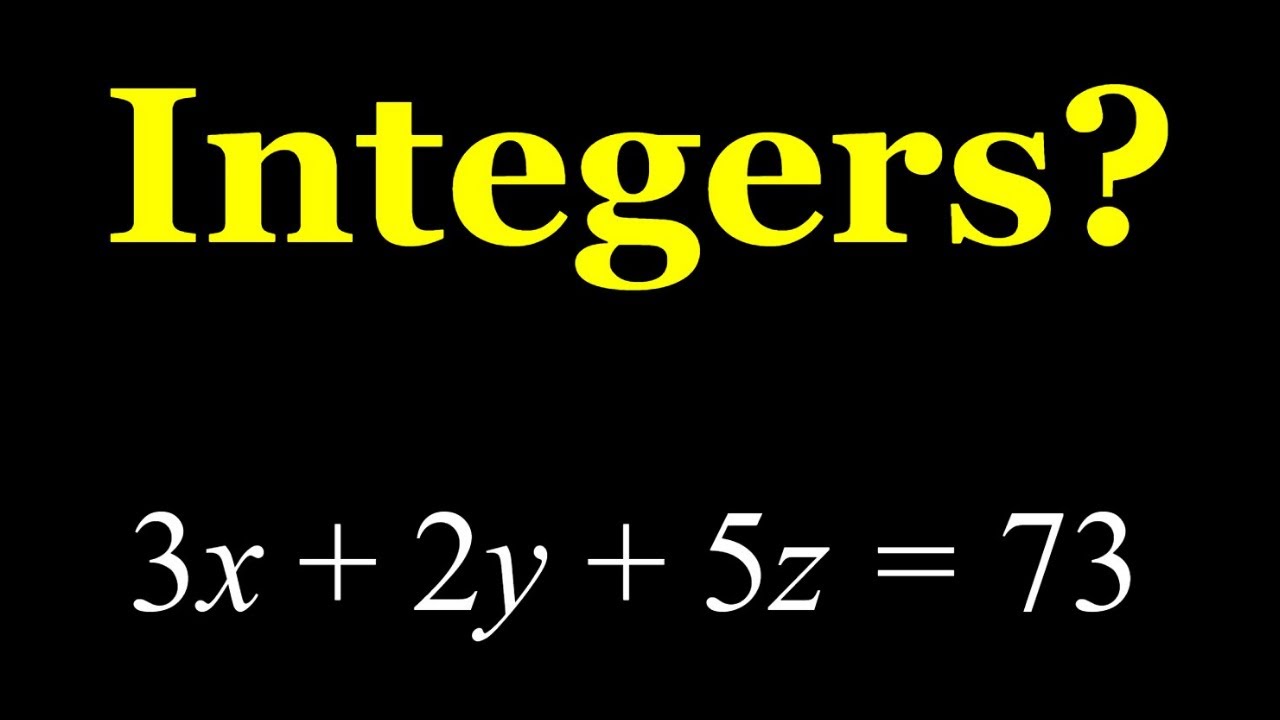
Показать описание
If you need to post a picture of your solution or idea:
#NumberTheoryProblems #DiophantineEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
#NumberTheoryProblems #DiophantineEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
Diophantine Equation: ax+by=gcd(a,b) ← Number Theory
A Nice Diophantine Equation in Number Theory | You Should Learn This Theorem | Math Olympiad
Number Theory | Linear Diophantine Equations
A Special Diophantine Equation in Number Theory with Special Formula You Need to Master
Linear Diophantine Equations | Road to RSA Cryptography #3
How To Solve Linear Diophantine Equations
Linear Diophantine Equation // Number Theory
A Linear Diophantine Equation
Find unit digit of 1! +2!+3!+•••••+50! | Number System | Linear Congruence
Linear Diophantine Equations with 3 Variables - 3 Different Methods
Using the Euclidean algorithm to find solutions to linear Diophantine equations - Ex 1
N1--Introduction to Linear Diophantine Equations
Linear Diophantine Equation |Examples |Number Theory
A Linear Diophantine Equation
How to Solve a Three Variable Linear Diophantine Equation
Diophantine Equations: Strategies and Examples
Finding the general solutions of the linear diophantine equation in an unique way!
N2--Solve Basic Linear Diophantine Equation
Finding all solutions to a linear Diophantine equation
Introduction to Solving Linear Diophantine Equations Using Congruence
Number Theory 34.1 - Linear Diophantine Equations: Example 1
A Linear Diophantine Equation | 3x+4y=17
Solving Linear Diophantine Equations - Simplified
Application of a Linear Diophantine Equation: Number of Stamps
Комментарии
 0:09:43
0:09:43
 0:07:40
0:07:40
 0:09:17
0:09:17
 0:08:10
0:08:10
 0:16:34
0:16:34
 0:10:24
0:10:24
 0:07:43
0:07:43
 0:10:24
0:10:24
 0:01:07
0:01:07
 0:17:43
0:17:43
 0:07:01
0:07:01
 0:05:11
0:05:11
 0:19:00
0:19:00
 0:00:27
0:00:27
 0:11:56
0:11:56
 0:27:34
0:27:34
 0:08:30
0:08:30
 0:08:48
0:08:48
 0:04:37
0:04:37
 0:06:38
0:06:38
 0:11:08
0:11:08
 0:00:47
0:00:47
 0:13:16
0:13:16
 0:05:12
0:05:12