filmov
tv
A Rational Equation with Integer Solutions (3/x)+(5/y)=4
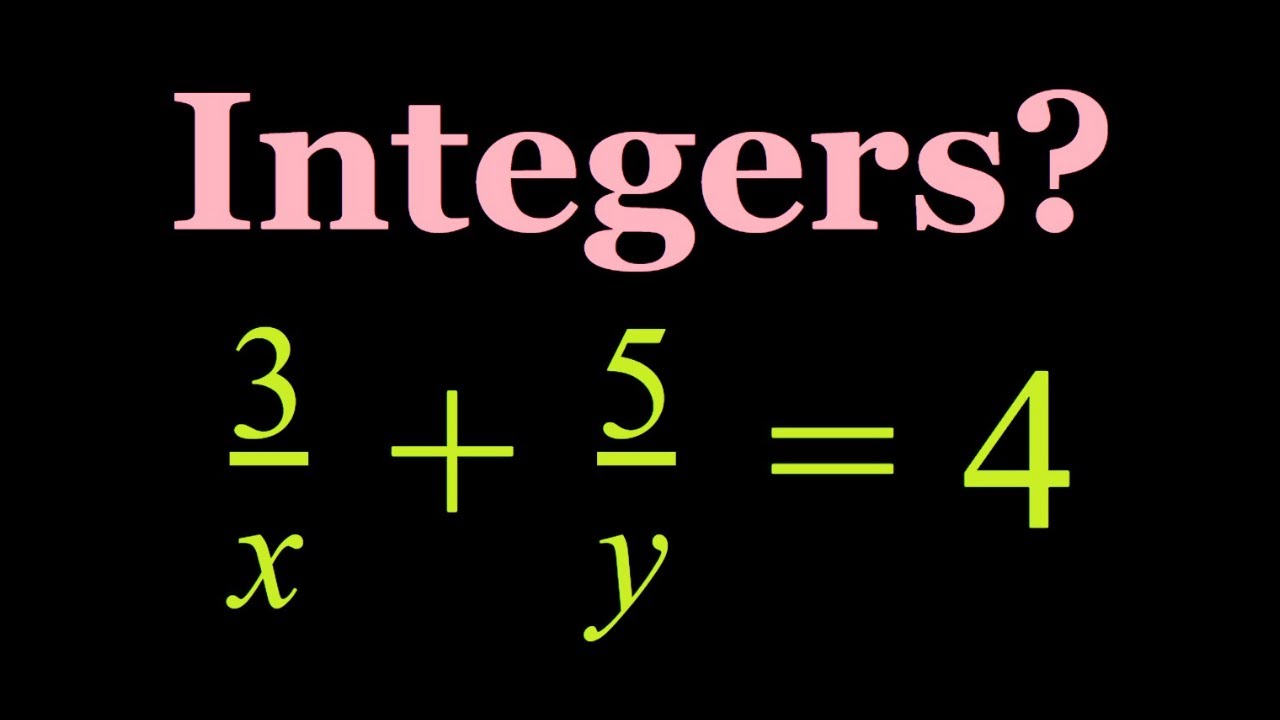
Показать описание
If you need to post a picture of your solution or idea:
#NumberTheoryProblems #DiophantineEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
#NumberTheoryProblems #DiophantineEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
A Rational Equation with Integer Solutions (3/x)+(5/y)=4
Solving Rational Equations
A Rational Equation with Positive Integers
A Rational Equation With Integers #maths #algebra #automobile
How to solve a Rational Equation with one solution
Solving a rational equation with two solutions
Ex: Solve a Rational Equation
Math tutorial for solving rational equations
Exponential equation. #maths #Mathematics #mathstutor #mathsisfun #exponential
Solving Rational Equation with Whole Number - Part 2 - General Mathematics
Solving a literal equation with a rational term
Solving a rational Equation
Solving a rational equation by factoring
Solving a rational Equation
Solving a rational Equation
Solving a basic rational equation by multiplying each term by the LCD
An Equation With Integer Solutions
Solving Rational Equations Easier Method
How To Solve Rational Equations In Easy Steps! Gen Math and Grade 8
Solve a Rational Equation with two solutions
Solve a rational equation by eliminating the denominators
A Rational Equation
Solving equations with rational expressions
Fun Rational Equation
Комментарии
 0:08:16
0:08:16
 0:11:03
0:11:03
 0:06:26
0:06:26
 0:00:31
0:00:31
 0:01:32
0:01:32
 0:08:50
0:08:50
 0:04:29
0:04:29
 0:06:32
0:06:32
 0:01:01
0:01:01
 0:07:20
0:07:20
 0:03:39
0:03:39
 0:05:33
0:05:33
 0:08:54
0:08:54
 0:02:56
0:02:56
 0:07:12
0:07:12
 0:04:12
0:04:12
 0:08:40
0:08:40
 0:04:33
0:04:33
 0:12:06
0:12:06
 0:01:23
0:01:23
 0:04:19
0:04:19
 0:08:20
0:08:20
 0:00:59
0:00:59
 0:01:32
0:01:32