filmov
tv
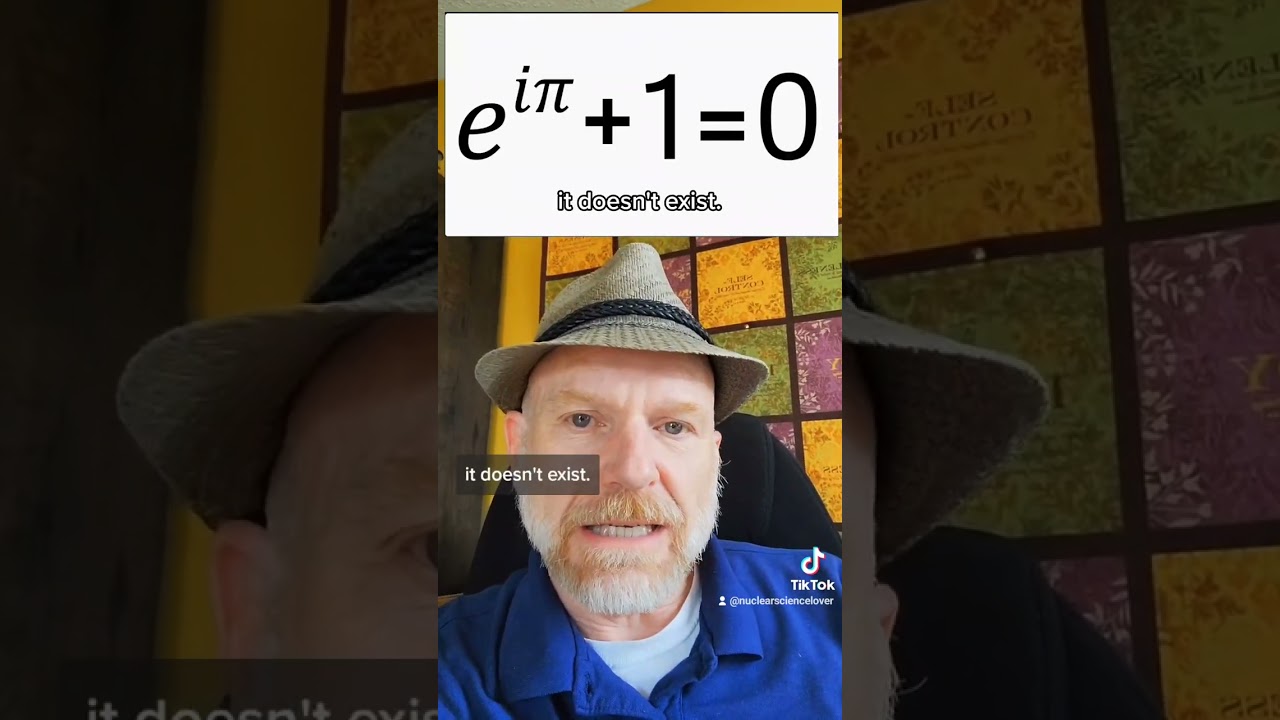
Euler's identity
Показать описание
e^(iπ) in 3.14 minutes, using dynamics | DE5
The Most Beautiful Equation
The Euler's formula explained!
Euler's identity
Euler's Identity (Complex Numbers)
Visualizing Euler's formula.
Euler’s identity proof for calculus 2 students!
Eulers formula
Proof of Euler's Formula Without Taylor Series
The most beautiful equation in math, explained visually [Euler’s Formula]
Euler's formula with introductory group theory
Someone asked me a question about Euler's Identity (e^iπ = --1)...
The Most Beautiful Equation in Math
A Golden Version Of Euler’s Identity
Your Daily Equation #11: Euler's Identity or The Most Beautiful of all Equations
Euler's formula & Euler's identity | Series | AP Calculus BC | Khan Academy
e (Euler's Number) - Numberphile
Euler's Formula Proof
Why do trig functions appear in Euler's formula?
Euler's Formula & Euler's Identity - Proof via Taylor Series
Euler's Formula - Numberphile
What is Euler's formula actually saying? | Ep. 4 Lockdown live math
Euler's Formula l Euler's Identity l Basic #calculus #basiccalculus
One of the Most Beautiful Equations: Euler's Identity
Комментарии
 0:04:08
0:04:08
 0:13:39
0:13:39
 0:00:33
0:00:33
 0:00:57
0:00:57
 0:13:32
0:13:32
 0:00:12
0:00:12
 0:07:19
0:07:19
 0:08:42
0:08:42
 0:03:57
0:03:57
 0:26:57
0:26:57
 0:24:28
0:24:28
 0:02:39
0:02:39
 0:03:50
0:03:50
 0:00:12
0:00:12
 0:26:20
0:26:20
 0:11:27
0:11:27
 0:10:42
0:10:42
 0:00:56
0:00:56
 0:13:11
0:13:11
 0:06:56
0:06:56
 0:21:23
0:21:23
 0:51:16
0:51:16
 0:00:10
0:00:10
 0:00:35
0:00:35