filmov
tv
Euler's Formula - Numberphile

Показать описание
More links & stuff in full description below ↓↓↓
NUMBERPHILE
Videos by Brady Haran
NUMBERPHILE
Videos by Brady Haran
Euler's Formula - Numberphile
e (Euler's Number) - Numberphile
The Euler's formula explained!
Incredible Formula - Numberphile
The mystery of 0.577 - Numberphile
e^(iπ) in 3.14 minutes, using dynamics | DE5
Euler Squares - Numberphile
What's so special about Euler's number e? | Chapter 5, Essence of calculus
Proof of Euler's Formula Without Taylor Series
Euler's formula with introductory group theory
The Most Beautiful Equation in Math
Euler’s Pi Prime Product and Riemann’s Zeta Function
What is Euler's formula actually saying? | Ep. 4 Lockdown live math
The Shortest Ever Papers - Numberphile
5 simple unsolvable equations
Euler's identity
Eulers formula
Euler's totient function | Journey into cryptography | Computer Science | Khan Academy
A proof that e is irrational - Numberphile
Euler's Formula Proof
Quaternions and 3d rotation, explained interactively
Euler Squares (extra) - Numberphile
A nice approach to Euler's formula
The World's Best Mathematician (*) - Numberphile
Комментарии
 0:21:23
0:21:23
 0:10:42
0:10:42
 0:00:33
0:00:33
 0:05:49
0:05:49
 0:10:03
0:10:03
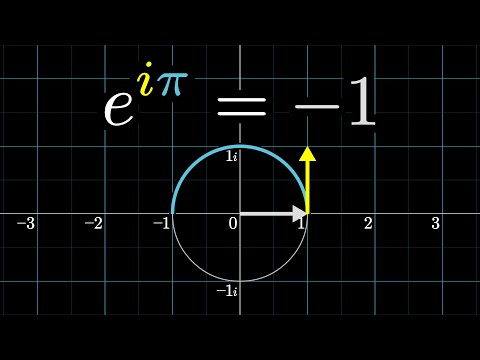 0:04:08
0:04:08
 0:15:27
0:15:27
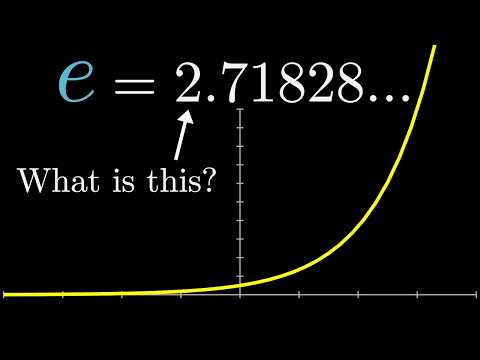 0:13:50
0:13:50
 0:03:57
0:03:57
 0:24:28
0:24:28
 0:03:50
0:03:50
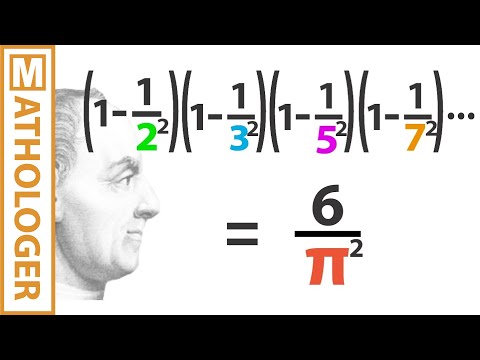 0:15:23
0:15:23
 0:51:16
0:51:16
 0:09:03
0:09:03
 0:00:50
0:00:50
 0:00:57
0:00:57
 0:08:42
0:08:42
 0:02:18
0:02:18
 0:16:29
0:16:29
 0:00:56
0:00:56
 0:05:59
0:05:59
 0:02:38
0:02:38
 0:00:39
0:00:39
 0:10:57
0:10:57