filmov
tv
Euler's Identity (Complex Numbers)
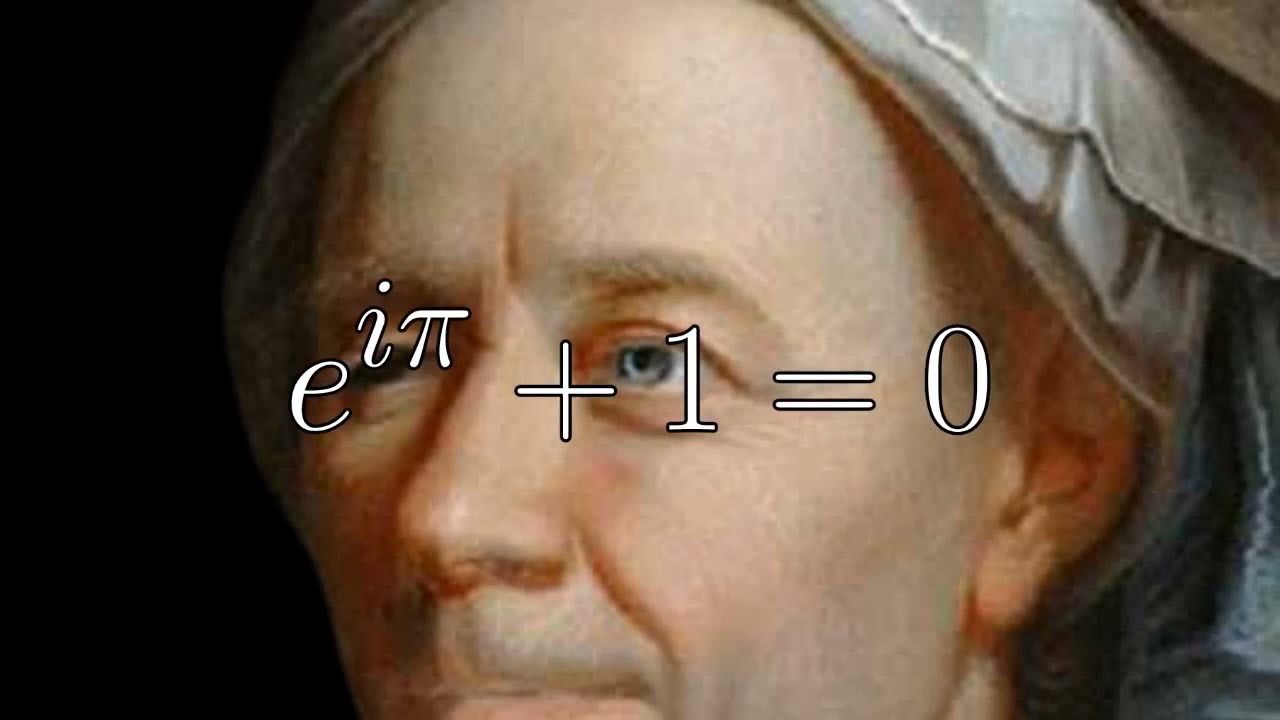
Показать описание
How the Fourier Transform Works, Lecture 4 | Euler's Identity (Complex Numbers)
In order to describe the Fourier Transform, we need a language. That language is the language of complex numbers. Complex numbers are a baffling subject but one that it is necessary to master if we are to properly understand how the Fourier Transform works. What is the imaginary number “i” and why it is so useful to us when dealing with the Fourier Transform?
This is the sixth in this series of videos which takes a new and visual look at the maths behind the magic of how the Fourier Transform works.
For a comprehensive and visually intuitive exploration of the Fourier Transform and its workings, I invite you to explore my book series on the Fourier Transform available at:
Click below to subscribe to the Course's mailing list to receive an update when the next video is available, updates about the course's production, and a notification of when the full course is available to purchase.
#math #mathematics #learning
Thanks for watching the video How the Fourier Transform Works, Lecture 4 | Euler's Identity (Complex Numbers)
In order to describe the Fourier Transform, we need a language. That language is the language of complex numbers. Complex numbers are a baffling subject but one that it is necessary to master if we are to properly understand how the Fourier Transform works. What is the imaginary number “i” and why it is so useful to us when dealing with the Fourier Transform?
This is the sixth in this series of videos which takes a new and visual look at the maths behind the magic of how the Fourier Transform works.
For a comprehensive and visually intuitive exploration of the Fourier Transform and its workings, I invite you to explore my book series on the Fourier Transform available at:
Click below to subscribe to the Course's mailing list to receive an update when the next video is available, updates about the course's production, and a notification of when the full course is available to purchase.
#math #mathematics #learning
Thanks for watching the video How the Fourier Transform Works, Lecture 4 | Euler's Identity (Complex Numbers)
Комментарии
 0:13:32
0:13:32
 0:08:42
0:08:42
 0:04:08
0:04:08
 0:00:33
0:00:33
 0:00:12
0:00:12
 0:26:57
0:26:57
 0:24:28
0:24:28
 0:03:57
0:03:57
 0:00:57
0:00:57
 0:03:50
0:03:50
 0:13:39
0:13:39
 0:51:16
0:51:16
 0:07:19
0:07:19
 0:06:06
0:06:06
 0:13:11
0:13:11
 0:29:57
0:29:57
 0:00:12
0:00:12
 0:21:23
0:21:23
 0:10:42
0:10:42
 0:14:34
0:14:34
 0:11:27
0:11:27
 0:05:15
0:05:15
 0:15:21
0:15:21
 0:00:35
0:00:35