filmov
tv
e^(iπ) in 3.14 minutes, using dynamics | DE5
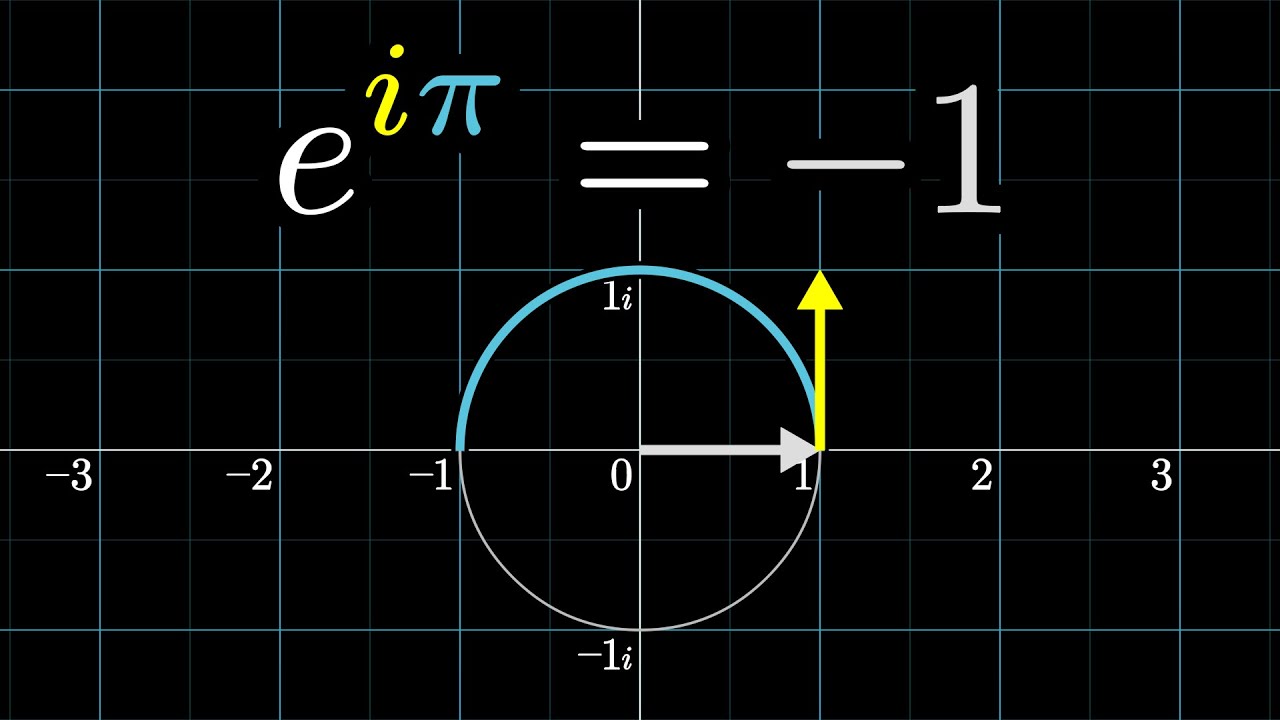
Показать описание
Euler's formula about e to the i pi, explained with velocities to positions.
An equally valuable form of support is to simply share some of the videos.
Not familiar with the calculus referenced in this video? Try taking a look at this one:
Another perspective on this formula, from Mathologer:
Another perspective from this channel:
And yet another from the blog Better Explained:
I'm not sure where the perspective shown in this video originates. I do know you can find it in Tristan Needham's excellent book "Visual Complex Analysis", but if anyone has a sense of the first occurrence of this intuition do feel free to share. It's simple and natural enough, though, that it's probably a view which has been independently thought up many times over.
Thanks to these viewers for their contributions to translations
Hebrew: Omer Tuchfeld
Vietnamese: @ngvutuan2811
------------------
If you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and it has many other quirks you might expect in a library someone wrote with only their own use in mind.
Music by Vincent Rubinetti.
Download the music on Bandcamp:
Stream the music on Spotify:
If you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.
------------------
Various social media stuffs:
An equally valuable form of support is to simply share some of the videos.
Not familiar with the calculus referenced in this video? Try taking a look at this one:
Another perspective on this formula, from Mathologer:
Another perspective from this channel:
And yet another from the blog Better Explained:
I'm not sure where the perspective shown in this video originates. I do know you can find it in Tristan Needham's excellent book "Visual Complex Analysis", but if anyone has a sense of the first occurrence of this intuition do feel free to share. It's simple and natural enough, though, that it's probably a view which has been independently thought up many times over.
Thanks to these viewers for their contributions to translations
Hebrew: Omer Tuchfeld
Vietnamese: @ngvutuan2811
------------------
If you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and it has many other quirks you might expect in a library someone wrote with only their own use in mind.
Music by Vincent Rubinetti.
Download the music on Bandcamp:
Stream the music on Spotify:
If you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.
------------------
Various social media stuffs:
Комментарии
 0:04:08
0:04:08
 0:06:14
0:06:14
 0:00:12
0:00:12
 0:03:50
0:03:50
 0:00:34
0:00:34
 0:03:24
0:03:24
 0:51:16
0:51:16
 0:03:57
0:03:57
 0:00:31
0:00:31
 0:13:50
0:13:50
 0:00:21
0:00:21
 0:13:11
0:13:11
 0:27:07
0:27:07
 0:00:58
0:00:58
 0:00:08
0:00:08
 0:11:05
0:11:05
 0:04:48
0:04:48
 0:03:16
0:03:16
 0:36:22
0:36:22
 0:14:03
0:14:03
 0:24:28
0:24:28
 0:08:37
0:08:37
 0:09:57
0:09:57
 0:19:13
0:19:13