filmov
tv
Euler's Formula & Euler's Identity - Proof via Taylor Series

Показать описание
Help me create more free content! =)
Euler's formula with introductory group theory
e^(iπ) in 3.14 minutes, using dynamics | DE5
Proof of Euler's Formula Without Taylor Series
Euler's Identity (Complex Numbers)
Euler's identity
Eulers formula
The Most Beautiful Equation
Euler's formula & Euler's identity | Series | AP Calculus BC | Khan Academy
Euler's Formula & Euler's Identity - Proof via Taylor Series
Euler’s identity proof for calculus 2 students!
Euler's Formula - Numberphile
The Most Beautiful Equation in Math
Why do trig functions appear in Euler's formula?
Euler's Identity : 'The Most Beautiful Equation Of Mathematics' #maths #euler
What is Euler's formula actually saying? | Ep. 4 Lockdown live math
Euler's Formula l Euler's Identity l Basic #calculus #basiccalculus
Someone asked me a question about Euler's Identity (e^iπ = --1)...
e (Euler's Number) - Numberphile
A Golden Version Of Euler’s Identity
Proof of Euler's Identity | Complex Numbers
13.Proof of Euler's Formula | Euler's Identity
Proving Euler's Identity FAST
Euler's identity
Euler's identity (e^ix= cos x + i sin x ) explained
Комментарии
 0:24:28
0:24:28
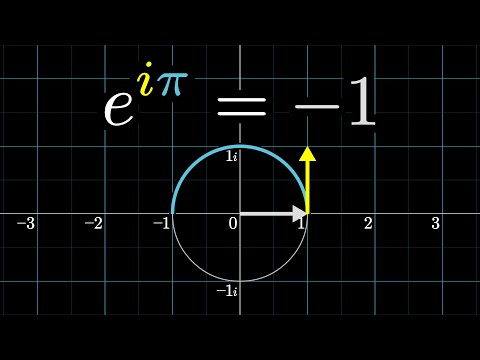 0:04:08
0:04:08
 0:03:57
0:03:57
 0:13:32
0:13:32
 0:00:57
0:00:57
 0:08:42
0:08:42
 0:13:39
0:13:39
 0:11:27
0:11:27
 0:06:56
0:06:56
 0:07:19
0:07:19
 0:21:23
0:21:23
 0:03:50
0:03:50
 0:13:11
0:13:11
 0:01:07
0:01:07
 0:51:16
0:51:16
 0:00:10
0:00:10
 0:02:39
0:02:39
 0:10:42
0:10:42
 0:00:12
0:00:12
 0:06:06
0:06:06
 0:07:03
0:07:03
 0:01:39
0:01:39
 0:00:26
0:00:26
 0:00:48
0:00:48