filmov
tv
Absolute Maximum and Minimum Values of Multivariable Functions - Calculus 3
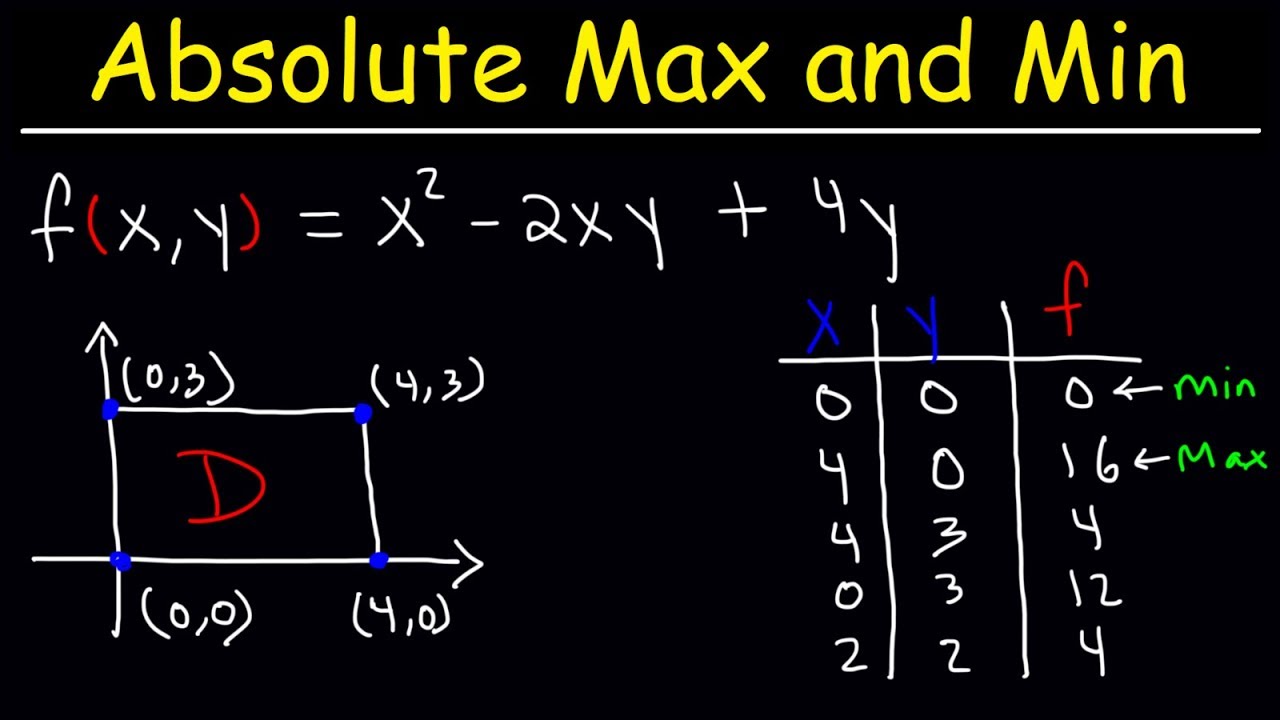
Показать описание
This Calculus 3 video tutorial explains how to find absolute maximum and minimum values given a multivariable function such as f(x,y). It explains how to find the critical points using partial derivatives and how to use the endpoints of rectangle D to find the absolute extrema.
Lines & Planes - Intersection:
Angle Between Two Planes:
Distance Between Point and Plane:
Chain Rule - Partial Derivatives:
Implicit Partial Differentiation:
________________________________
Directional Derivatives:
Limits of Multivariable Functions:
Double Integrals:
Local Extrema & Critical Points:
Absolute Extrema - Max & Min:
________________________________
Lagrange Multipliers:
Triple Integrals:
2nd Order - Differential Equations:
Undetermined Coefficients:
Variation of Parameters:
________________________________
Final Exams and Video Playlists:
Full-Length Videos and Worksheets:
Lines & Planes - Intersection:
Angle Between Two Planes:
Distance Between Point and Plane:
Chain Rule - Partial Derivatives:
Implicit Partial Differentiation:
________________________________
Directional Derivatives:
Limits of Multivariable Functions:
Double Integrals:
Local Extrema & Critical Points:
Absolute Extrema - Max & Min:
________________________________
Lagrange Multipliers:
Triple Integrals:
2nd Order - Differential Equations:
Undetermined Coefficients:
Variation of Parameters:
________________________________
Final Exams and Video Playlists:
Full-Length Videos and Worksheets:
Комментарии
 0:11:24
0:11:24
 0:17:17
0:17:17
 0:06:18
0:06:18
 0:25:26
0:25:26
 0:09:15
0:09:15
 0:03:27
0:03:27
 0:05:21
0:05:21
 0:12:42
0:12:42
 3:06:20
3:06:20
 0:11:19
0:11:19
 0:18:57
0:18:57
 0:07:42
0:07:42
 0:01:00
0:01:00
 0:16:37
0:16:37
 0:08:34
0:08:34
 3:38:16
3:38:16
 0:02:41
0:02:41
 0:04:08
0:04:08
 0:09:23
0:09:23
 0:14:18
0:14:18
 0:20:02
0:20:02
 0:10:19
0:10:19
 0:08:51
0:08:51
 0:06:17
0:06:17