filmov
tv
Visual Group Theory, Lecture 3.6: Normalizers
Показать описание
Visual Group Theory, Lecture 3.6: Normalizers
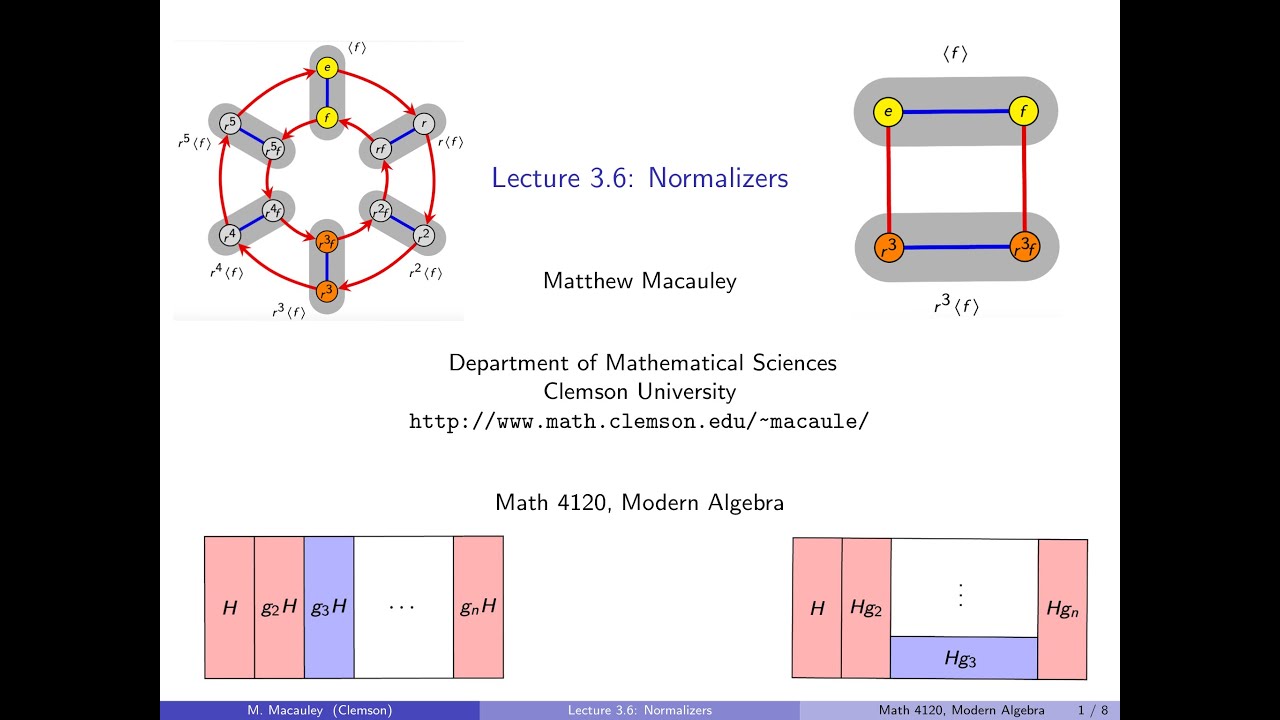
A subgroup H of G is normal if xH=Hx for all x in G. If H is not normal, then the normalizer is the set of elements for which xH=Hx. Obviously, the normalizer has to be at least H and at most G, and so in some sense, this is measuring "how close H is to being normal". We interpret this in terms of Cayley diagrams, and then prove some basic properties of normalizers: they are always subgroups, and they are unions of cosets -- precisely, those left cosets that are also right cosets.
A subgroup H of G is normal if xH=Hx for all x in G. If H is not normal, then the normalizer is the set of elements for which xH=Hx. Obviously, the normalizer has to be at least H and at most G, and so in some sense, this is measuring "how close H is to being normal". We interpret this in terms of Cayley diagrams, and then prove some basic properties of normalizers: they are always subgroups, and they are unions of cosets -- precisely, those left cosets that are also right cosets.
0:38:20
Visual Group Theory, Lecture 6.3: Polynomials and irreducibility
0:39:19
Visual Group Theory, Lecture 3.7: Conjugacy classes
0:40:38
Visual Group Theory, Lecture 3.5: Quotient groups
0:31:29
Visual Group Theory, Lecture 6.6: The fundamental theorem of Galois theory
0:24:34
Visual Group Theory, Lecture 4.6: Automorphisms
0:29:50
Visual Group Theory, Lecture 2.3: Symmetric and alternating groups
0:44:05
Visual Group Theory, Lecture 5.3: Examples of group actions
0:26:28
Visual Group Theory, Lecture 6.5: Galois group actions and normal field extensions
0:26:34
Visual Group Theory, Lecture 6.1: Fields and their extensions
0:34:13
Visual Group Theory, Lecture 6.4: Galois groups
0:30:45
Visual Group Theory, Lecture 2.1: Cyclic and abelian groups
0:19:11
Visual Group Theory, Lecture 3.2: Cosets
0:23:16
Visual Group Theory, Lecture 3.4: Direct products
0:18:48
Permutations, Latin squares, number systems | Group theory episode 3
0:36:34
Visual Group Theory, Lecture 5.7: Finite simple groups
0:35:41
Visual Group Theory, Lecture 6.2: Field automorphisms
0:21:58
Group theory, abstraction, and the 196,883-dimensional monster
0:44:44
Lecture 3 || Composition Table, Addition Modulo, Multiplication Modulo || B.A. / B.Sc. Mathematics
0:22:46
Visual Group Theory, Lecture 6.7: Ruler and compass constructions
0:33:27
Visual Group Theory, Lecture 1.2: Cayley graphs
0:35:57
Group Theory: Lecture 21/30 - Conjugacy Classes of the Alternating Group
0:13:40
Chapter 3: Lagrange's theorem, Subgroups and Cosets | Essence of Group Theory
0:01:00
The Group Theory Used to Solve the Hardest Differential Equation
0:00:48
How small are atoms?
Комментарии