Visual Group Theory, Lecture 4.6: Automorphisms

Visual Group Theory, Lecture 4.6: Automorphisms

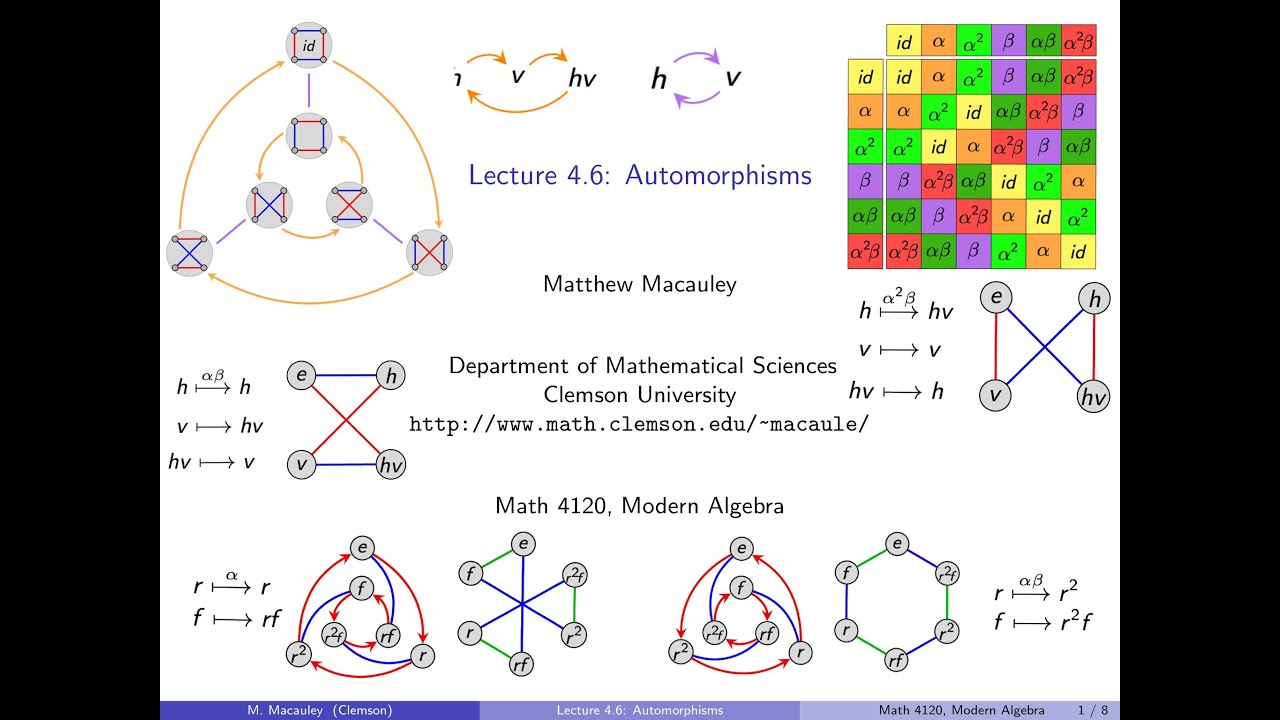
An automorphism is an isomorphism from a group to itself. The set of all automorphisms of G forms a group under composition, denoted Aut(G). After a few simple examples, we learn how Aut(Z_n) is isomorphic to U(n), which is the group consisting of set of integers relatively prime to n, where the operation is multiplication modulo n. Next, we look at automorphisms of both the dihedral group D_3 and the Klein 4-group V_4, and see how they can be thought of as "re-wirings" of the Cayley diagram. In both of these cases Aut(G) is a non-abelian group of order 6.

[gamesmathandmusic]

gonna be going through this playlist. Nice way of looking at automorphisms as rewirings - very appealing.

[BSplitt]

There is an error at 10:00. It should be Z_5 -> Z_5, not Z_4 -> Z_4

[artemshlyakhtov]

Wow. So multiplicative operations are just automorphism groups in some sense. This even works for infinite sets, like the rational numbers.

[Mrpallekuling]

In this video, I cannot find this:
A mapping G->G is an automorphism of G is:
- f is a bijection.
- f(ab) = f(a)f(b) for all a and b in G (for me, this was helpful in the calculations in this video)
Is there a reason for this?

[olegdats]

Z4->Z4, f(1)E{ 1, 2, 3, 4} maybe is should be {1, 3}? |Aut(Z4)|=2

[The_Pi_Piper]

I have one question....
Automorphism of Dn is isomorphic to which group ??
(Here Dn is dihedral group).
I have only idea of its order.... Order of Aut(Dn) is n × phi(n).

[tutorpedia]

How to find number of automorphism of Z2×Z2×Z2

[ThefamousMrcroissant]

Please FOR THE LOVE OF GOD stop SMACKING and making wet noises in the microphone. It's with all these online lectures. It's impossible to listen to for people with mysophonia.