filmov
tv
A function f: R→ R satisfies that equation f(x + y) = f(x) f(y). Prove that f^ prime (x) = 2f(x)
Показать описание
Dr. Debprasad Majumder
🎯Problem:
A function f: R→ R satisfies that equation f(x + y) = f(x) f(y) for all x, yeR, f(x) 0. Suppose that the function f(x) is differentiable at x = 0 and f' (0) = 2. Prove that f^ prime (x) = 2f(x) .
🎯Problem:
A function f: R→ R satisfies that equation f(x + y) = f(x) f(y) for all x, yeR, f(x) 0. Suppose that the function f(x) is differentiable at x = 0 and f' (0) = 2. Prove that f^ prime (x) = 2f(x) .
0:03:00
A function f: ℝ⇒ℝ defined by f(x)= x²+3 is
0:08:35
Show that the function f: R* to R* defined by f(x)=1/x is one-one and onto. If the domain R* is N
0:03:41
Show that the Modulus function f: R to R, given by f(x)=|x| is neither one-one nor onto|CBSE|NCERT|
0:06:29
A function f: R→ R satisfies that equation f(x + y) = f(x) f(y). Prove that f^ prime (x) = 2f(x)
0:05:12
Let the function f:R to R be defined by f(x)=2x+sinx, then f is one one onto or not
0:07:52
Function: Example 11 Show that f:R to R, defined as f(x)=x^2,is neither one-one nor onto.
0:01:43
Show that a function f : R → R given by f(x) = ax + b, a, b ∊ R, a 0 is a bijective....
0:07:18
Let A=R-{3}&B=R-{1}Consider the function f:A to B defined by f(x)=(x-2/x-3) Is f one-one & o...
1:04:48
Learn to Code in R - 7 Things you Should Know
0:08:20
In each of the following cases, state whether function is one-one, onto or bijective f:R-R f(x)=3-4x
0:01:36
'Show that the exponential function `f: R-R` , given by `f(x)=e^x` , is one-one but not onto.
0:03:16
Prove that the Greatest Integer function f: R to R given by f(x)=[x] is neither one-one nor onto
0:04:48
A function f:R+ →R (where R+ is the set of all non negative real numbers) defined by f(x)=4x+3 is
0:02:30
Show that the function f : R → R given by f(x) = x^3 is injective.
0:04:08
Show that the signum function f: R to R, given by f(x)=1 if x≥0; 0 if x=0;-1, if x≤0 is neither
0:04:42
Let the function : f 𝐑→𝐑 to be defined by f(x)= cos x for all x ∈𝐑. Show that ' f ' is nei...
0:07:19
'The function `f: R- R` defined by `f(x)=2^x+2^(|x|)` is (a) one-one and onto
0:01:01
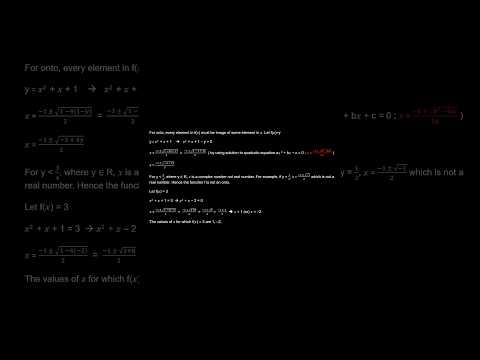
Show that a function f: R to R defined by f(x) = x^2 + x + 1 is neither one-one nor onto.
0:01:42
If R is the set of real numbers and a function `f: R to R ` is defined as `f(x)=x^(2), x in R
0:02:16
A function `f: R to R` is defined as: `f(x) ={{:(1,x in Q)
0:01:59
'Prove that the greatest integer function `f: R-R` , given by `f(x)=[x]` , is neither
0:04:15
The function f: R → R, f(x)=x^2 is (a) injective but not surjective (b) surjective but not inject......
0:05:32
Define the function f : R `->,` R by y = f(x) = `x^2` , `x in R` . Complete the Table given be...
0:03:13
Show that the function `f;R-.R` defined by `f(x)=cos(5x+2)` is neither one-one nor onto ?
Комментарии