filmov
tv
Solving Linear Differential Equations with an Integrating Factor (Differential Equations 16)

Показать описание
Examples of solving Linear First Order Differential Equations with an Integrating Factor.
Remember that when we have to divide by X, we should be stating a condition we are placing on the differential equation. TYPICALLY, this is x greater than 0. I will take this for granted in this video. It SHOULD be stated when rewriting a differential equation. So, even though I take it for granted (and probably should have written that), YOU SHOULD DEFINITELY be writing that condition on your paper.
First Order Linear Differential Equation & Integrating Factor (introduction & example)
First Order Linear Differential Equations
How to Solve First Order Linear Differential Equations
The Method of Integrating Factors for Linear 1st Order ODEs **full example**
Solving Linear Differential Equations with an Integrating Factor (Differential Equations 16)
Linear Differential Equations & the Method of Integrating Factors
Finding particular linear solution to differential equation | Khan Academy
🔵15 - Linear Differential Equations: Initial Value Problems (Solving Linear First Order ODE's)...
BSC Math Lecture: Unit 2 Lecture 04 - ODE Semester 3 Lucknow University #lucknowuniversity #bsc #nep
Second Order Linear Differential Equations
Class 12th – Procedure to solve Linear Differential Equations | Tutorials Point
Systems of linear first-order odes | Lecture 39 | Differential Equations for Engineers
First order, Ordinary Differential Equations.
How to use the Integrating Factor Method (First Order Linear ODE)
Introduction to Linear Differential Equations and Integrating Factors (Differential Equations 15)
The Bernoulli Equation // Substitutions in Differential Equations
8: Eigenvalue Method for Systems - Dissecting Differential Equations
Solving First-Order Linear Differential Equations - Introduction with Examples
Separable First Order Differential Equations - Basic Introduction
Differential equations, a tourist's guide | DE1
How to Solve Constant Coefficient Homogeneous Differential Equations
How To Solve First Order Homogeneous Differential Equation
Difference between linear and nonlinear Differential Equation|Linear verses nonlinear DE
solve differential equation with substitution
Комментарии
 0:20:34
0:20:34
 0:22:28
0:22:28
 0:10:53
0:10:53
 0:05:07
0:05:07
 1:11:01
1:11:01
 0:11:36
0:11:36
 0:06:30
0:06:30
 0:21:16
0:21:16
 0:38:58
0:38:58
 0:25:17
0:25:17
 0:02:04
0:02:04
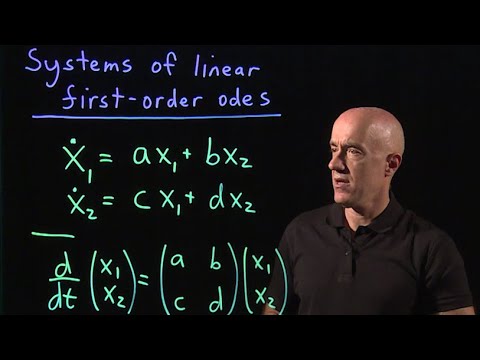 0:08:28
0:08:28
 0:48:35
0:48:35
 0:03:44
0:03:44
 1:07:16
1:07:16
 0:09:19
0:09:19
 0:08:57
0:08:57
 0:09:26
0:09:26
 0:10:42
0:10:42
 0:27:16
0:27:16
 0:06:41
0:06:41
 0:08:33
0:08:33
 0:03:29
0:03:29
 0:05:36
0:05:36