filmov
tv
The Method of Integrating Factors for Linear 1st Order ODEs **full example**

Показать описание
In this video we do a full example using the method of integrating factors to solve a first order differential equation. The first thing to observe is that this is a linear ODE. Then, we apply the integral formula to get the integrating factor, and finally use that to get a solution to the ODE.
OTHER COURSE PLAYLISTS:
OTHER PLAYLISTS:
► Learning Math Series
►Cool Math Series:
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
SOCIALS:
The Method of Integrating Factors for Linear 1st Order ODEs **full example**
Linear Differential Equations & the Method of Integrating Factors
Method of Integrating Factor
How to use the Integrating Factor Method (First Order Linear ODE)
First Order Linear Differential Equation & Integrating Factor (introduction & example)
First Order Linear Differential Equations
Oxford Calculus: Integrating Factors Explained
Solving Linear Differential Equations with an Integrating Factor (Differential Equations 16)
The Integrating Factor Method
Deriving the method of integrating factors
ODE | Integrating factors general method
The Method of Integrating Factors
🔵13 - Non Exact Differential Equations and Integrating Factors 1
The Integrating Factor Method | Solving First Order Linear Differential Equations
First order ODEs - Integrating factor method
Linear Differential Equations & Integrating Factors - Intro
Introduction to Linear Differential Equations and Integrating Factors (Differential Equations 15)
How to Solve First Order Linear Differential Equations
First-Order Linear Differential Equations & Integrating Factors (Introduction)
Integrating Factors
Solving a first order linear diff eq (integrating factor, method of undetermined coefficient)
Integrating factors - method and example
Differential Equations Integrating factor type (Examples) : ExamSolutions Maths Tutorials
DFQ - Chapter 2.1: Method of Integrating Factors
Комментарии
 0:05:07
0:05:07
 0:11:36
0:11:36
 0:09:14
0:09:14
 0:03:44
0:03:44
 0:20:34
0:20:34
 0:22:28
0:22:28
 0:21:35
0:21:35
 1:11:01
1:11:01
 0:09:55
0:09:55
 0:11:55
0:11:55
 0:04:43
0:04:43
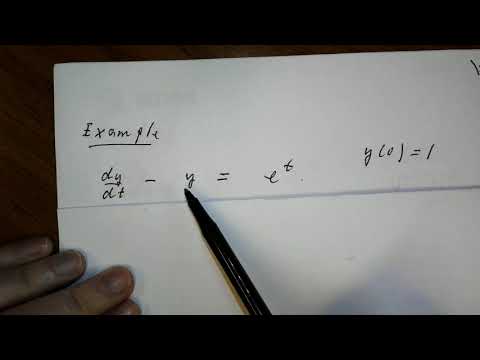 0:11:47
0:11:47
 0:18:11
0:18:11
 0:19:12
0:19:12
 0:05:17
0:05:17
 0:14:38
0:14:38
 1:07:16
1:07:16
 0:10:53
0:10:53
 0:12:05
0:12:05
 0:11:02
0:11:02
 0:18:43
0:18:43
 0:08:59
0:08:59
 0:11:19
0:11:19
 0:38:57
0:38:57