filmov
tv
How To Solve First Order Homogeneous Differential Equation
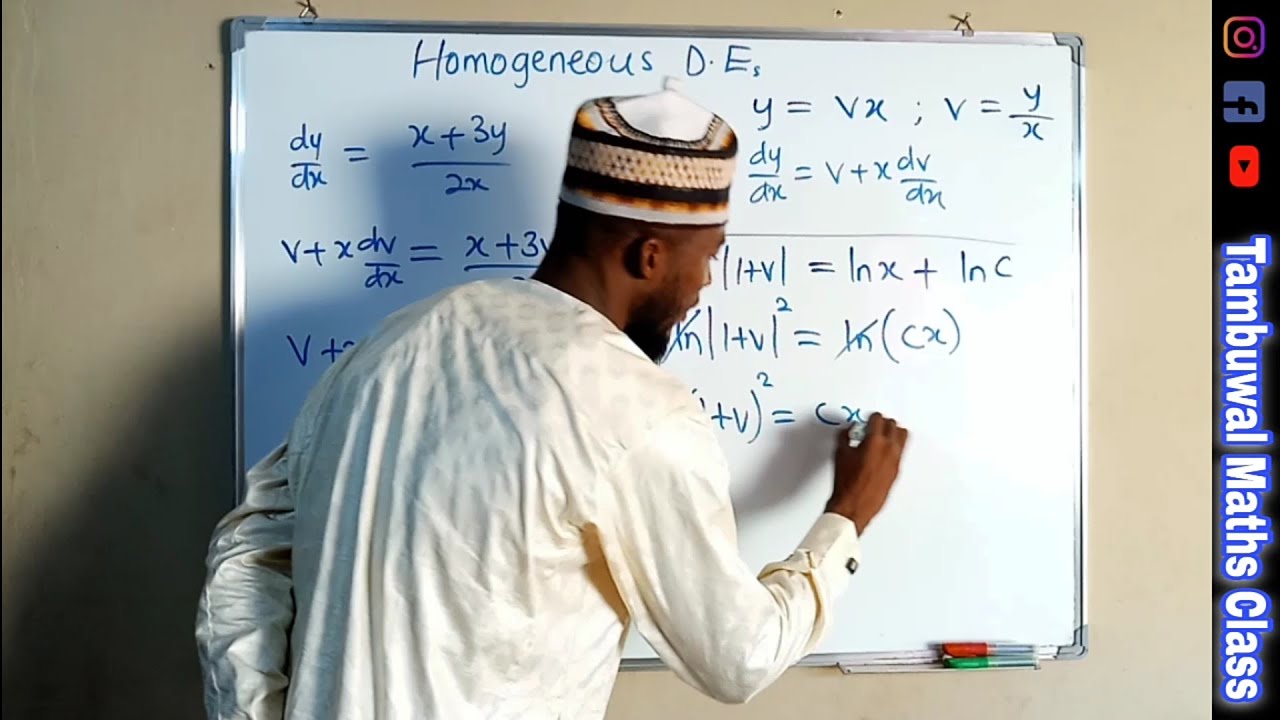
Показать описание
This looks simple enough, but we find that we cannot express the RHS in the form of 'x-factors' and 'y-factors', so we cannot solve by the method of separating the variables.
In this case we make the substitution y = vx, where v is a function of x. So y = vx. Differentiate with respect to x (using the product rule): dy/dx = v+x(dv/dx)
then you substitute for y and dy/dx in the main equation thereby transforming the Equation in to separable type.
Note: dy/dx =(x+3y)/2x is an example of a #homogeneous #differential #equation. This is determined by the fact that the total degree in x and y for each of the terms involved is the same (in this case, of degree 1). The key to solving every homogeneous equation is to substitute y = vx where v is a function of x. This converts the equation into a form which we can solve by separating the variables.
If you find this video interesting, kindly subscribe to my channel for more exciting Maths tutorials.
In this case we make the substitution y = vx, where v is a function of x. So y = vx. Differentiate with respect to x (using the product rule): dy/dx = v+x(dv/dx)
then you substitute for y and dy/dx in the main equation thereby transforming the Equation in to separable type.
Note: dy/dx =(x+3y)/2x is an example of a #homogeneous #differential #equation. This is determined by the fact that the total degree in x and y for each of the terms involved is the same (in this case, of degree 1). The key to solving every homogeneous equation is to substitute y = vx where v is a function of x. This converts the equation into a form which we can solve by separating the variables.
If you find this video interesting, kindly subscribe to my channel for more exciting Maths tutorials.
0:22:28
First Order Linear Differential Equations
0:10:53
How to Solve First Order Linear Differential Equations
0:05:07
The Method of Integrating Factors for Linear 1st Order ODEs **full example**
0:48:35
First order, Ordinary Differential Equations.
0:20:34
First Order Linear Differential Equation & Integrating Factor (introduction & example)
0:10:42
Separable First Order Differential Equations - Basic Introduction
0:08:33
How To Solve First Order Homogeneous Differential Equation
0:07:49
Differential equation introduction | First order differential equations | Khan Academy
0:00:00
Differential Equation Solution: How to solve Differential Equations by Variable Separation method.
0:02:46
Solving an Exact Differential Equation
0:03:44
How to use the Integrating Factor Method (First Order Linear ODE)
0:06:57
4 Types of ODE's: How to Identify and Solve Them
0:05:08
❖ Solving Separable First Order Differential Equations ❖
0:42:08
Learning First Order Linear DE in 30 Minutes!
0:11:36
Linear Differential Equations & the Method of Integrating Factors
0:12:05
First-Order Linear Differential Equations & Integrating Factors (Introduction)
0:19:40
Exact differential equation (introduction & example)
0:05:46
Initial Value Problem
0:23:37
How to Solve Differential Equations in PYTHON
0:06:40
Exact First Order Differential Equations - Part 1
0:09:52
How to solve a first order linear differential equation with integrating factors
0:12:31
First Order Circuits and RC Circuit Example
0:01:23
Class 12th – Procedure to Solve First Order First Degree Differential Equation | Tutorials Point
0:06:48
How to Solve 1st Order Inhomogeneous ODE's?
Комментарии